Introduction
Diffusion-weighted magnetic resonance imaging (DWI)
has been established as an important non-invasive technique for
probing and characterizing the microstructure of living tissue
in vivo (1). While probing
the capability of water to diffuse in various directions and
scales, multiple 3-dimentional (3D) DWIs have been acquired using
echo-planar imaging (EPI). However, the spatial resolution and
signal-to-noise ratio (SNR) is limited by several physical,
clinical and economical considerations (2). Poor spatial resolution in fact poses
significant limits on the scale of tissue structure that may be
characterized by DWI. For instance, individual axon diameters are
in the order of 1–30 µm, while the typical DWI resolution is ~2×2×2
mm3, which only provides summative measures from
millions of axons. In addition, the partial volume effect also
limits the DWI to the investigation of the major fiber bundles in
the brain (3). Therefore, increasing
spatial resolution of DWI is beneficial for reducing partial volume
effects, which allows fine details of the tissue structure to be
resolved and characterized with enhanced certainty (4).
Several methods have been proposed to increase the
spatial resolution of DWI, and may be broadly divided into two
categories: The acquisition procedure and the post-processing
procedure. Increasing spatial resolution through image acquisitions
typically involves the use of high-quality diffusion gradient
coils, and a longer echo time (TE) that is necessary for encoding a
larger k-space in a single shot. However, increasing TE leads to
increased error accumulations during spatial encoding and enhanced
geometric and intensity distortion along the phase encoding
direction (5). Alternatively, higher
magnetic fields (7 Tesla or more) may be employed, which offers an
effective solution to improving SNR while reducing image distortion
caused by larger spatial encoding (6). Other methods have also been proposed
for improving spatial resolution, for instance, using a
specifically designed gradient coil such as Gradient Insert
(7). While all these methods require
a hardware upgrade in the scanner, methods that are based on
changing image acquisition schemes for the purpose of improving
spatial resolution are also available. A representative method of
this type is anisotropic orthogonal acquisition, which employs a
maximum of a posteriori estimations from multiple scans to exploit
spatial homogeneity and provide regularized solutions for isotropic
high-resolution (HR) (8).
Enhancing spatial resolution in the post-processing
procedures shares the common concept as the well-known
super-resolution (SR) technology, which was developed for the same
problem in video sequences (9). A
preliminary study on SR of DWI data was performed by Peled and
Yeshurun (2), who resorted to a set
of spatially shifted DWI for enhanced spatial resolution. Later,
Arsigny et al (10)
introduced Log-Euclidean metrics into interpolation of diffusion
tensor magnetic resonance imaging (DTI) data, which naturally
allows for tensor super-resolution. Furthermore, Calamante et
al (11) proposed a tract
density imaging-based method that weighs the interpolation with
tract density, which elegantly achieves an appealing visualization
effect.
Intuitively, the resolution of DWI may be enhanced
by adapting state-of-the-art SR methods from simple scene images,
such as the non-local method (12)
and overcomplete dictionaries (13).
However, as pointed out in numerous DWI applications (14–16), due
to the particular nature of DWI data, only a combination of
multiple channels may reveal the complex structure of white matter,
since a single channel simply captures partial information
regarding the underlying neuronal structure. In the present study,
a novel SR method for a multiple-channel DWI dataset was proposed
based on a well-known non-local mean filter. The proposed method
introduced joint information, which encapsulates the intrinsic
similarity redundancy of adjacent DWI channels, to improve the
regularization of the SR procedure. In addition, an efficient
rotational invariant similarity measure was also applied to the
proposed SR method. This not only increased the redundant pattern,
which is beneficial for more accurate HR image reconstruction, but
also reduced the computational burden for more practical
applications.
A preliminary version of the proposed method was
first described in a conference paper (17). The present study consolidated this
work and expanded on the results. The proposed SR method is
described in detail in the method section. After quantitative and
qualitative comparison of the proposed SR framework on a synthetic
and a real DWI dataset, the advantages and limitations of the
proposed technique were discussed.
Materials and methods
Methods
To recall the problem of SR, it may be assumed that
the low-resolution (LR) image Y corresponds to the original HR
image X according to the following model:
Y=DHX+η
where H is the degradation operator, D
is the decimation operator and η is additive noise. The SR
reconstruction problem is to estimate the underlying HR version X
from Y as follows:
Xˆ=argminX||Y–DHX||2+λℜ(X)
where ℜ(X)
inline is a regulation term and λ is the regulation parameter that
balances the fidelity term and regulation term.
A non-local strategy has been proposed primarily as
an efficient denoising method (18),
and was then adapted to multiply modifications (12,19–21). In
addition to denoising applications, the non-local method may also
be adapted for an SR reconstruction task (12,22–24). In
these applications, the patch-based non-local estimator was used to
define the regulation term:
ℜ(X)=∑p∈Ω||Xp–Xˆp||
where X̂p is acquired with a
non-local estimator:
Xˆp=∑q∈ωw(Xp,Xq)Xq
in which Xp and
Xq are the voxels at location p and
q, respectively, ω is a searching window and w weighs
the similarity betweenpatches S(Xp) and S(Xq) as below:
w(Xp,Xq)=1Zpe–||S(Xp)–S(Xq)||2h2
where h is the decay parameter and
Zp is a normalization constant that is defined as
the sum of all the weights.
As previously reported (12), after computing this regularization
term, the fidelity term is then applied for subsampling consistency
(25):
Yp–1L∑i=1LXˆp=0,∀p∈Y
Finally, this non-local interpolation framework is
implemented iteratively until convergence, and this two-step
iteration may be defined as follows:
Xˆpt+1=1Zp∑q∈we–||S(Xpt)–S(Xqt)||2h2Xqt
Xˆt+1=Xˆt+1–NN(DHXˆt+1–Y)
where NN is the nearest neighbor interpolation, and
t is the iteration number. Equations 7 and 8
correspond to the non-local reconstruction and mean correction,
respectively.
This non-local SR method was proposed primarily for
3D MRI, and was then adapted for DWI application, which uses
non-diffusion image (b0) information as the HR reference to
guide the reconstruction (24).
Of note, joint information, as indicated previously,
gathers the information from all correlated gradient images,
providing extra redundancy, which is beneficial for SR
reconstruction.
XNp and
XNq denote the DWI patches,
with N corresponding to the Nth gradient direction.
Due to the fact that DWI is stored sequentially, an adjacent
gradient direction is associated with a higher correlation. As
previously reported (19,21), a more efficient non-local estimation
may be acquired through a more accurate weighting scheme.
Intuitively, it is possible for joint information from correlation
gradient directions to improve weighting accuracy, which leads to
better SR reconstruction:
(XˆpN)t+1=∑q∈ww((XpN)t,(XqN)t)(XqN)t
w((XpN)t,(XqN)t)=1Zpexp{–(||S(XpN–k)–S(XqN–k)||2h2+…+||S(XpN)–S(XqN)||2h2+…+||S(XpN+k)–S(XqN+k)||2h2)}
where k=round(n–12), with n being a
constant resembling the number of gradient directions.
It should be noted that the similarity measure in
equation 10 is not rotationally
invariant. As previously pointed out (19,20), the
rotationally invariant measure may be applied to the proposed SR
method for further improvement of the HR image reconstruction.
Manjon et al (19) proposed a
simple but effective rotationally invariant measure, which is based
on voxel intensity and the corresponding patch means. The present
study we adopted this rotationally invariant measure into a
non-local SR method with joint information of DWI, so that the
similarity measure in equation 10 may be rewritten as follows:
w((XpN)t,(XqN)t)=1Zpexp{–(||S(XpN–k)–S(XqN–k)||2h2+…+||S(XpN)–S(XqN)||2h2+…+||S(XpN+k)–S(XqN+k)||2h2+3||μ((XpN)n)–μ((XqN)n)||2h2)}
where µ is the mean of the patches around voxel
XNp (or
XNq) and its corresponding
n nearby gradient directions.
As presented in equation 8, the mean correction step in order to
ensure that the reconstructed HR image is consistent with the
original LR image is as follows:
(XˆN)t+1=(XˆN)t+1–NN(DH(XˆN)t+1–Y)
where NN is the nearest neighbor interpolation,
H is the degradation operator, D is the decimation
operator and X̂N is the reconstructed HR image.
Experiments
A synthetic dataset, a high-field in vivo
DWI dataset and a physical phantom dataset were selected to
evaluate the proposed method. Regarding the use of the in
vivo dataset, the study was approved by the ethics committee of
Vanderbilt University Institutional Review Board (Nashville, TN,
USA). Prior to experiments, written informed consent was obtained
from the participant. In addition, different interpolation methods
and super-resolution methods were also involved for comparison. The
first is B-spline interpolation, which was introduced for DWI
resolution enhancement in the literature (26,27) and
was used for comparison. A non-local approach for MRI
super-resolution (12) was also
involved for comparison, together with the proposed method
implementing joint information (Proposed-n) and rotationally
invariant similarity measure (Proposed-RI-n). For the methods used
in the present study, all scenarios were tested (n=1, 3, 5),
since using more gradients becomes computationally prohibitive. As
presented in equation 10, if
n=1, the algorithm is simplified to the classical non-local
method. The searching window was set as suggested in (12), and the decremental approach alone was
used in the convergence process to define the delay parameter
h (24).
The simulation dataset consists of the 3D structure
field presented at the 2012 high-angular resolution diffusion
imaging (HARDI) Reconstruction Challenge (28) and has a 16×16×5 volume attempting to
simulate a realistic 3D configuration of tracts occurring. As
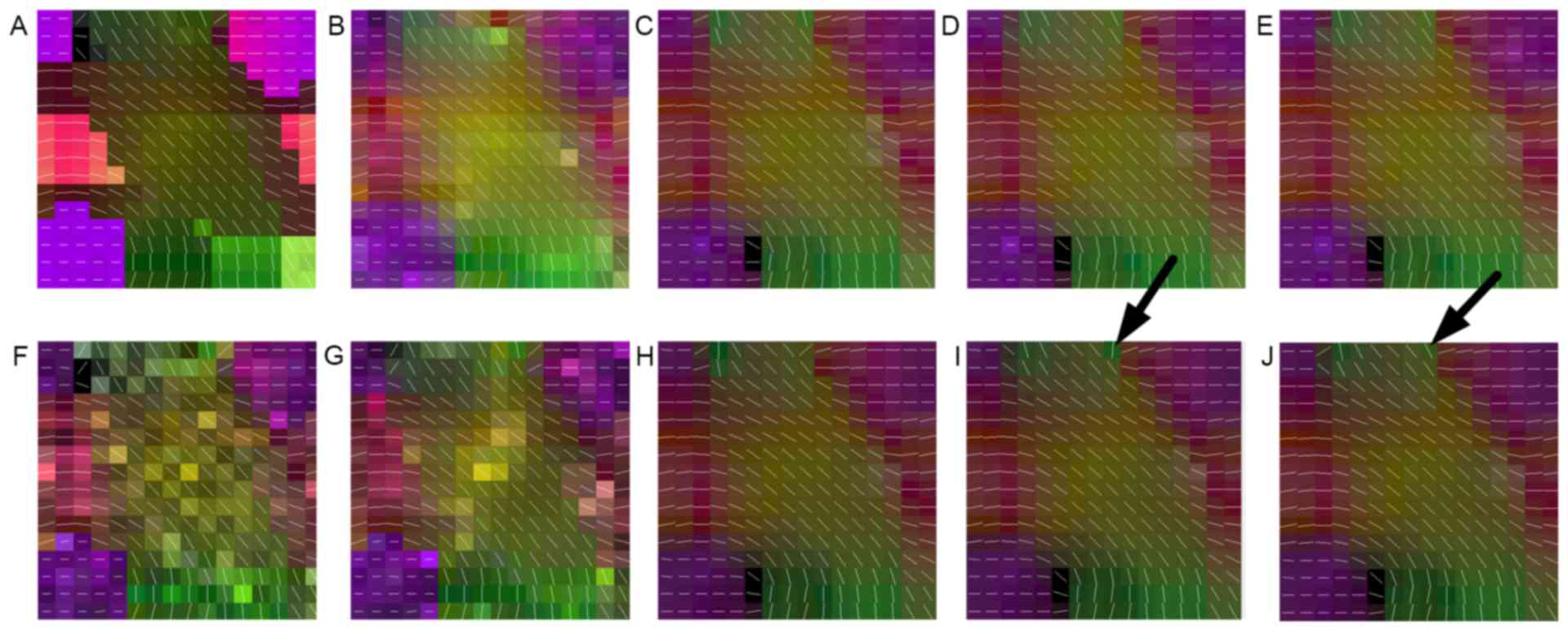
presented in Fig. 1A, this dataset
is comprised of five different fiber bundles, which gave rise to
the nonplanar configurations of bending, crossing and kissing
tracts. All fiber tracts were characterized with a fractional
anisotropy between 0.75 and 0.90. To better explore the proposed
method, this synthetic dataset was also corrupted by Rician noise
(SNR, 30) and displayed in Fig. 1F.
The original dataset and the noisy one were down-sampled by a
factor of 2 using the nearest neighbor interpolation along each
axis. Next, the LR datasets were super-resolved using the B-spline
method, the non-local method, and the proposed methods with 5
directions. In addition to the visual comparison demonstrated in
Fig. 1, the angular accuracy was
also involved for quantitative evaluation (28). The angular accuracy in the
orientation of the estimated fiber compartments was assessed by
means of the average error (in degrees) between the estimated fiber
directions and the true ones present in a voxel:
θ¯=180πarccos(|dtrue×destimated|)
where the unitary vectors dtrue and destimated are
a true fiber population in the voxel and the ones closest to the
estimated directions.
The in vivo DWI dataset was acquired by a 7T
Philips Achieva whole-body scanner (Philips Healthcare, Cleveland,
OH, USA) with a volume head coil for transmission and 32-channels.
A DW dual spin-echo, SENSE accelerated multi-shot EPI was used to
acquire the DWI data (b-value, 700 sec/mm2; 15 diffusion
directions; field of view, 210×210×30 mm3; matrix size,
300×300 with 15 slices and a spatial resolution of 0.7×0.7×2
mm3). A gold standard image was constructed based on
this in vivo HR DWI dataset to quantitatively and
qualitatively validate the proposed approach. For this, 10
acquisitions of HR DW images were averaged in the image space
(0.7×0.7×2 mm3). The LR images used for the experiment
were then simulated by down-sampling the gold standard by a factor
of 2 using the nearest neighbor interpolation along each axis,
i.e., [2 2 2], which resulted in simulated LR images of 1.4×1.4×4
mm3. The HR and LR data were filtered using the UNLM3D
filter to remove random noise prior to HR reconstruction. Two
objective measure matrixes, namely the Peak SNR (PSNR) and the
structural similarity (SSIM) (29)
were used to quantitatively evaluate the super-resolved DWI
dataset. The PSNR measures the differences between each of the
images and the image quality, while the SSIM measures the structure
and perceptual similarities between the original and reconstructed
images.
SSIM(x,y)=(2μxμy)(2σxy+c2)(μx2+μy2+c1)(σx2+σy2+c2)
where µx and µy are the mean value of images × and
y, Σx and Σy are the standard deviation of × and y, respectively,
Sxy is the covariance between them, and constants c1 and
c2 were set as suggested in a previous study (29).
For further investigation, a physical phantom
dataset used in tracking analysis was also implemented. As proposed
in previous studies (30,31), this phantom dataset was scanned in
two spatial resolutions; a dataset with a resolution of 6×6×6
mm3 was selected for interpolation and a dataset with a
resolution of 3×3×3 mm3 was used for comparison.
Finally, a diffusion tensor image (32) and a HARDI model using spherical
deconvolution (33) were
reconstructed using the super-resolved DWI dataset for evaluation
in a quantitative as well as a qualitative manner. For a synthetic
phantom, the diffusion tensor field and principal eigenvector were
computed using CAMINO (34) and are
displayed in Fig. 1. Table I presents the mean and standard
deviation of the angular error estimated by equation 13. For the in vivo dataset, the
DWI reconstruction results were quantitatively and qualitatively
compared in Figs. 2 and 3, respectively, followed by comparison of
the effect of motion artifacts and geometric distortions in
Figs. 4 and 5. Fractional anisotropy (FA), the
FA-weighted color map of the principal eigenvector and the
principal eigenvector of the estimated tensor and were determined
and displayed in Figs. 6, 7 and 8,
respectively. For the physical phantom dataset, the orientation
distribution function (ODF) using spherical deconvolution (33) was estimated and displayed in Fig. 9.
 | Table I.Angular error on estimated tensors in
original phantom and noisy phantom (signal-to-noise ratio, 30)
using B-spline, non-local upsampling and proposed method. |
Table I.
Angular error on estimated tensors in
original phantom and noisy phantom (signal-to-noise ratio, 30)
using B-spline, non-local upsampling and proposed method.
| Phantom | B-Spline angular
error (°) | Non-local angular
error (°) | Proposed-5 grad
angular error (°) | Proposed-RI-5
angular error (°) |
|---|
| Original |
8.6±24.5 |
7.4±20.5 |
7.2±20.3 |
7.0±20.1 |
| Noisy |
14.2±31.2 |
12.6±32.7 |
12.3±32.4 |
12.1±32.1 |
All experiments were performed on a personal
computer running MATLAB R2013b (Mathworks, Natick, MA, USA) in
Windows 7, with an Intel(R) core i7-4600 U processor and 8 GB
RAM.
Results
Simulation results
Fig. 1 demonstrates
the principal eigenvector of the tensor model in the synthetic
phantom and the results of the reconstruction performed using the
above-mentioned methods. It was indicated that the proposed methods
outperformed the interpolated method in noisy as well as no-noise
situations. By carefully observing Fig.
1E and J, it may be observed that the proposed method achieved
more robust reconstruction results with no irregular tensors, as
indicated by arrows. This was also in accordance with the
quantitative comparison of the angular error in Table I, in which the proposed method
achieved the most accurate reconstruction results of tensor
direction in the original and noisy datasets.
In vivo dataset results
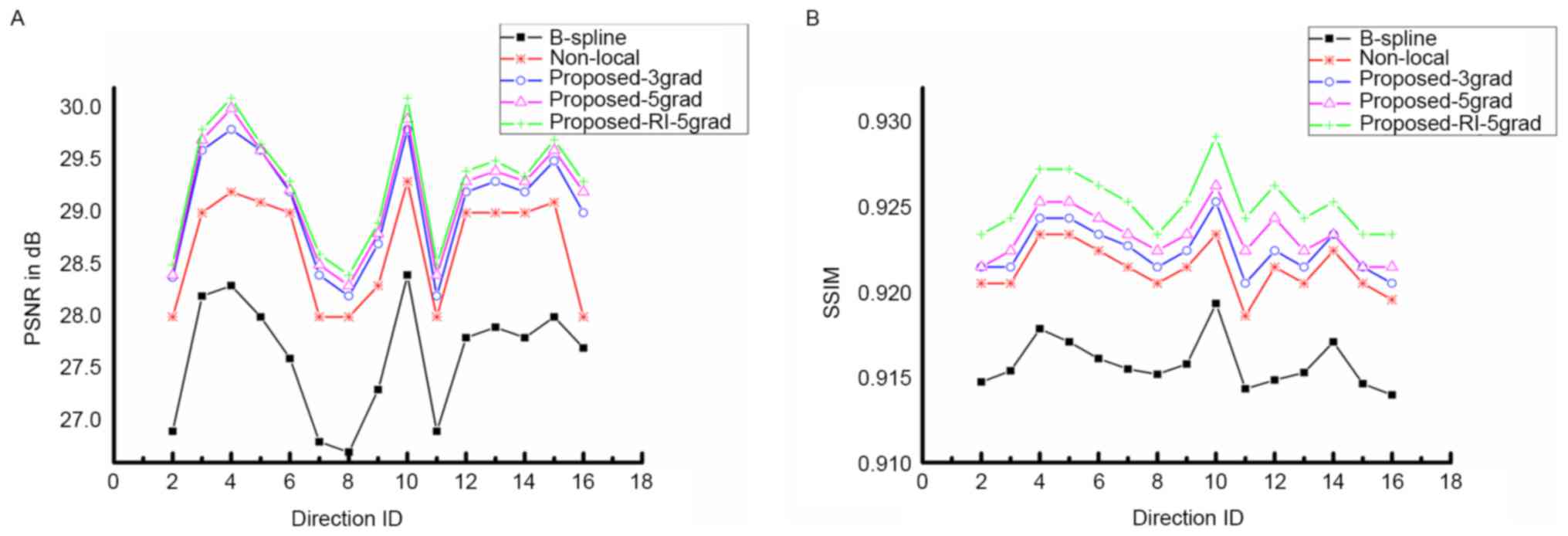
The quality of DWI reconstruction is demonstrated
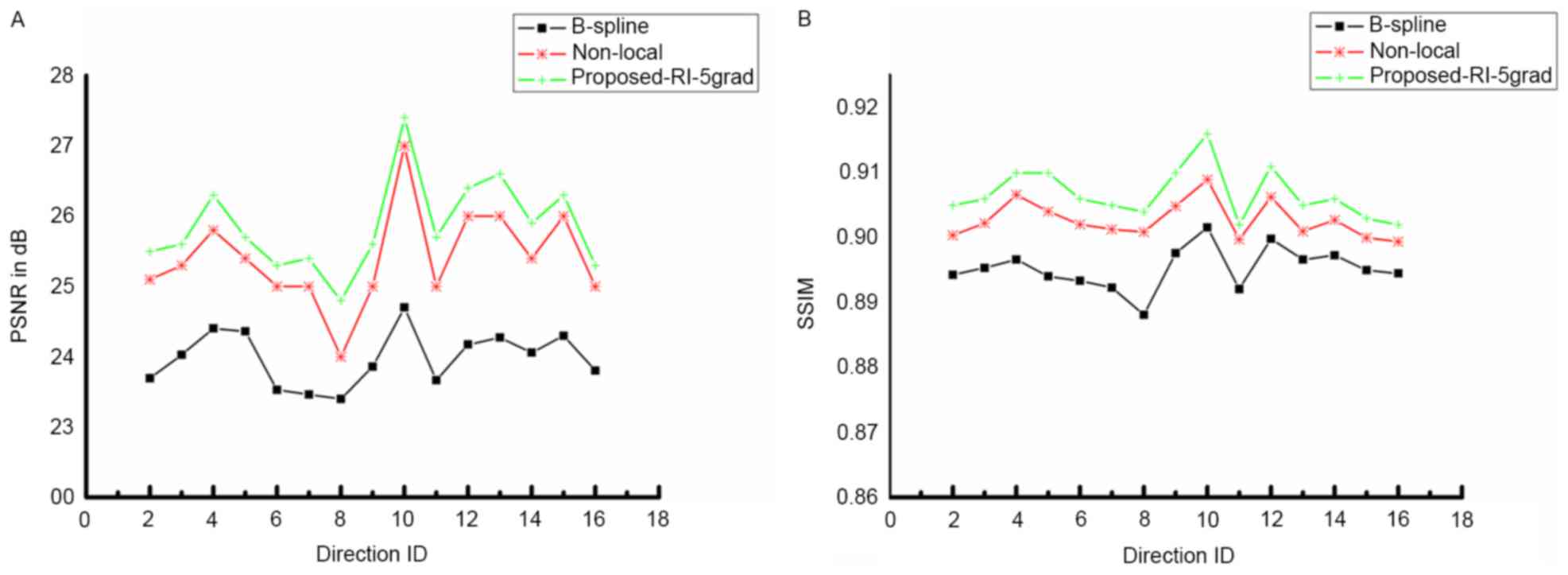
in Figs. 2 and 3. Fig. 2
presents the PSNR and SSIM of the proposed method compared with
B-spline interpolation and non-local upsampling (12). As indicated in the study by Manjón
et al (12), the patch-based
method was better than the classical interpolation. For the
proposed method of the present study, the super-resolution using
joint information enhanced the reconstructed image quantitatively
for every DWI image with different directions. In addition, PSNR as
well as SSIM improved with the increasing involvement of nearby DWI
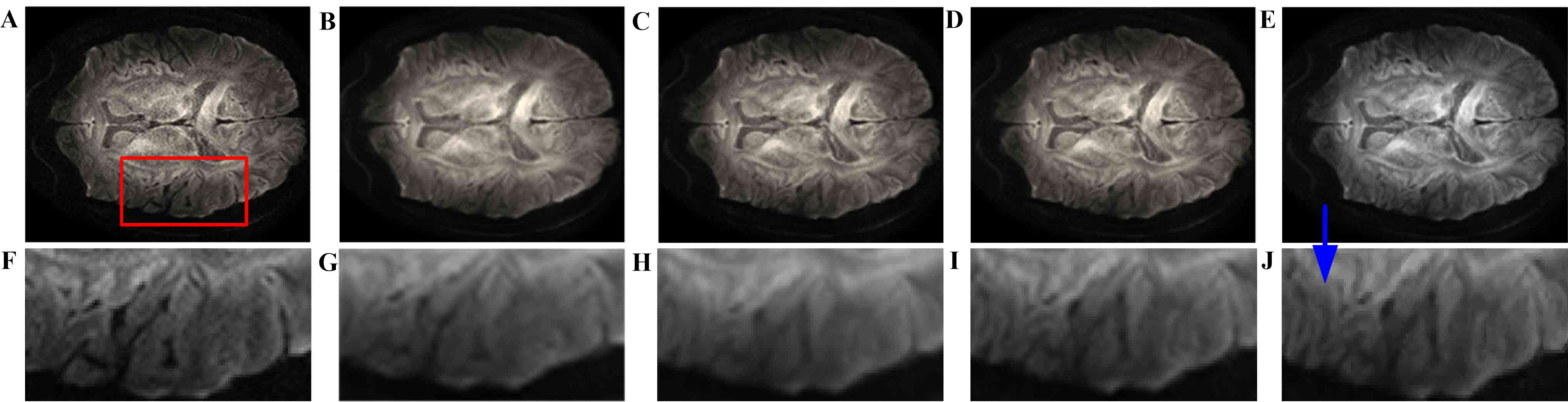
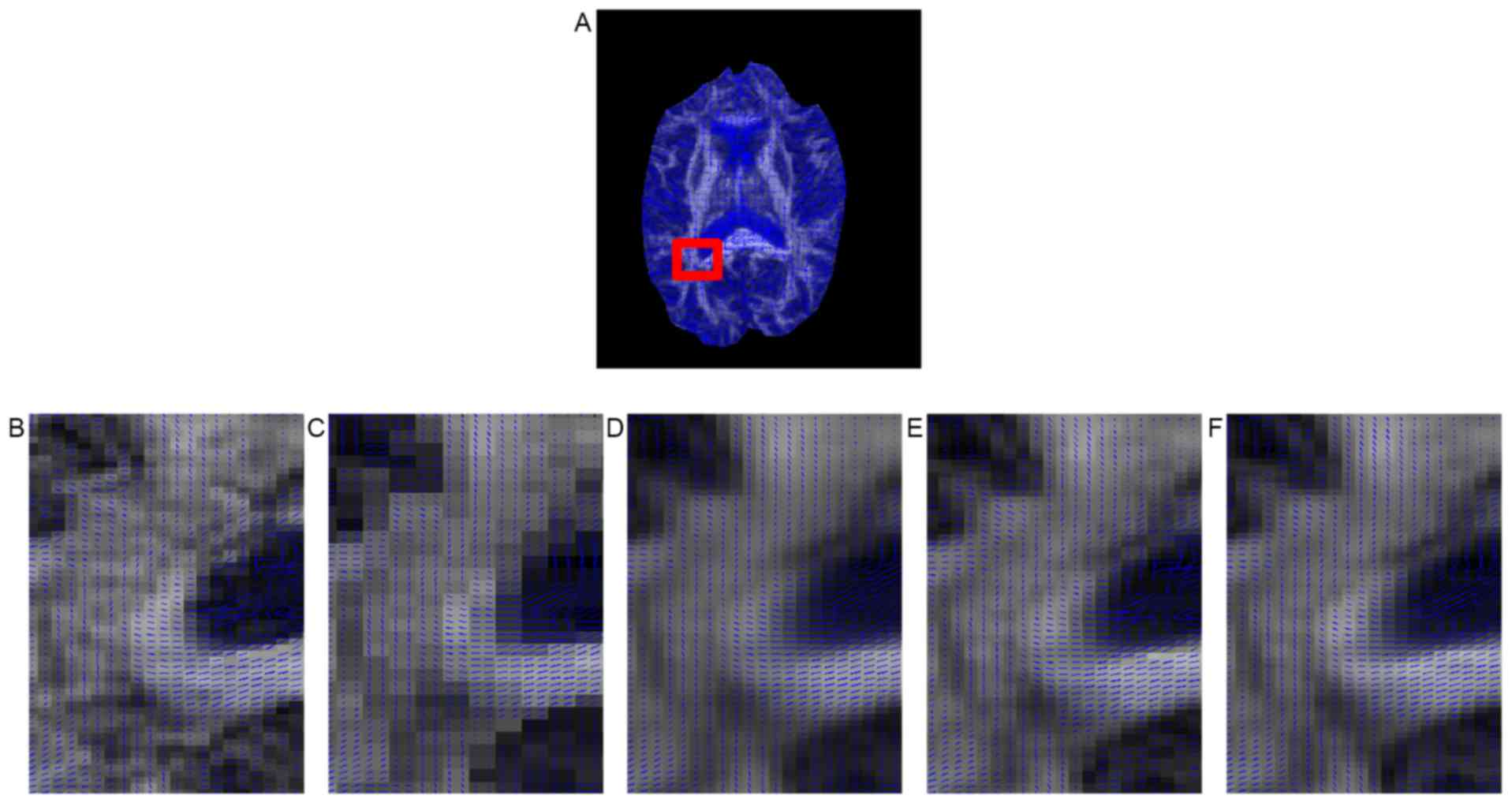
images. Fig. 3 presents the visual
comparison of the reconstructed DWI images. The reconstructed image
(Fig. 3B) had the blurriest result
of all, while the proposed method using seven nearby gradient
images (Fig. 3E) achieved the image
most similar to the golden standard (Fig. 3A). The crack in the enlarged region
demonstrates that using joint information, the proposed-RI-5 grad
(Fig. 3E) reconstructed the best
spatial features of the cracked area as indicated by the blue
arrow, compared with the same area reconstructed by other methods,
in which the edges are blurry and difficult to distinguish.
As indicated by Coupé et al (24), DWI datasets are vulnerable to motion
artifacts and geometric distortions. Therefore, the impact of
misalignments on the quality of results using the proposed method
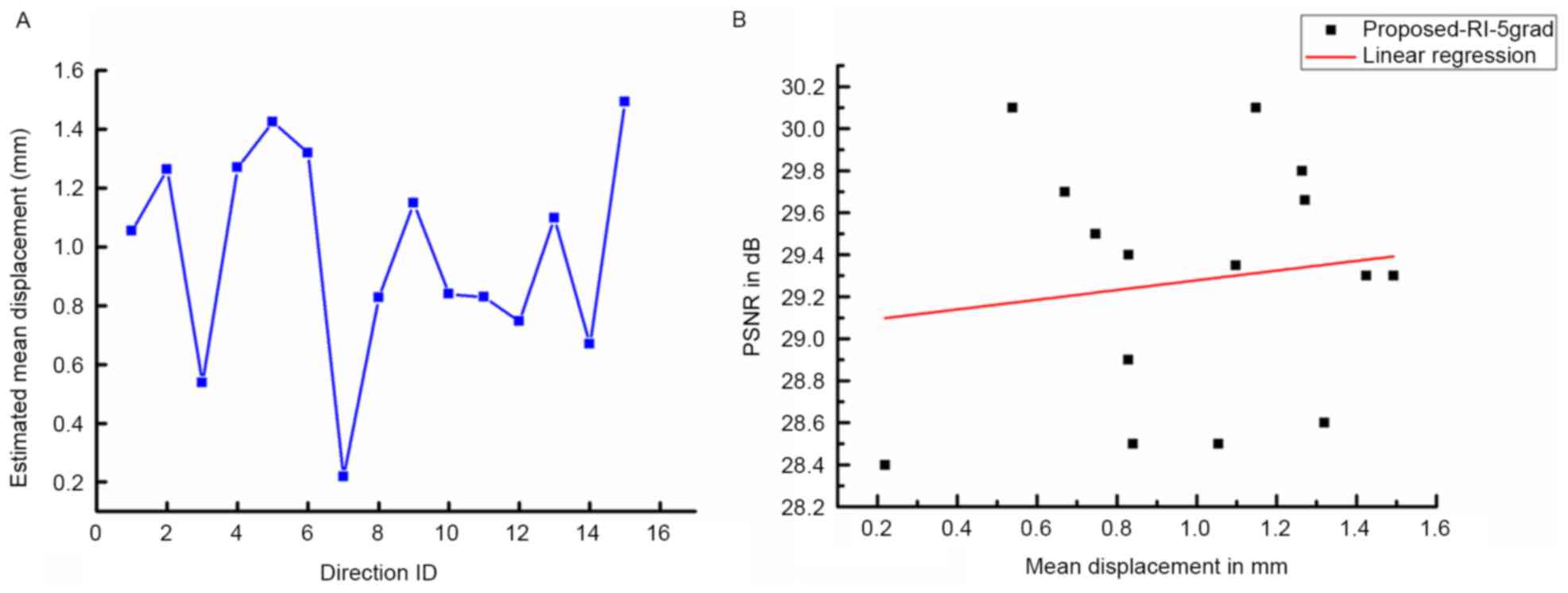
was studied. First, the displacements between b0 and DW images were
obtained with an FSL eddy current correction (35) and the mean displacements estimated
from the reconstruction results are displayed in Fig. 4A. Fig.
4B demonstrates the correlation between image quality in terms
of PSNR and the estimated mean displacements. No significant linear
correlation between the results from the proposed method and the
estimated mean displacements was observed, which demonstrates the
robustness of the proposed method towards the limited
misalignment.
The impact of distortion corrections on the results
of the proposed method was also studied in Fig. 5. The experiment in Fig. 1 was repeated using the corrected
dataset, and data were then subjected to the FSL eddy current
correction. Subsequently, the PSNR and SSIM of the results using
B-spline, non-local upsampling and the proposed method were
computed using the corrected gold standard and presented in
Fig. 5.
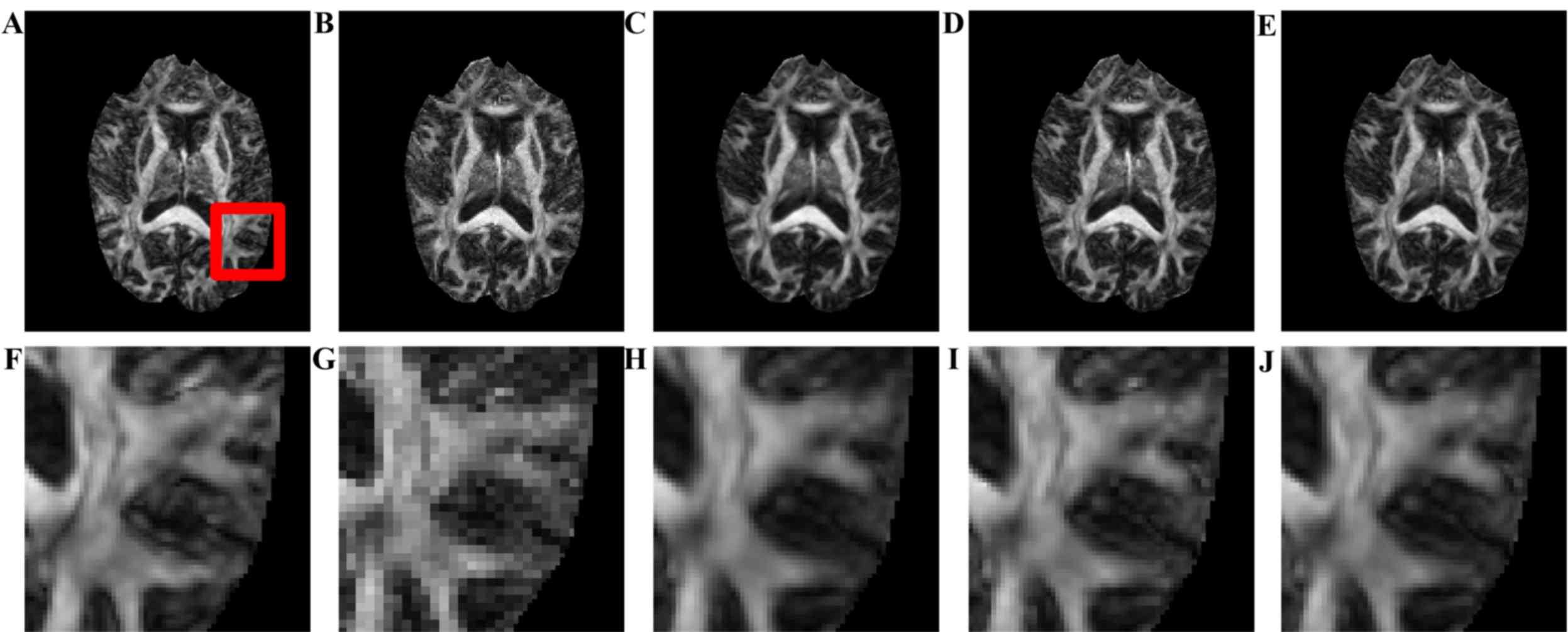
Figs. 6 and 7 demonstrate the FA map and color map,
respectively, of the estimated DTI data from the reconstructed DWI.
Table II presents the PSNR and SSIM
of the FA map. Consistent with Figs.
2 and 3, the FA and color map
estimations using B-spline interpolation were worst among all
methods. Following careful observation of the results in the boxed
areas, it became apparent that the proposed method provides a
better estimation for FA, application of the upsampling method
resulted in coarse edges and the proposed method reconstructed the
highest volume corresponding to the gold standard image. For the
anterior horn of the lateral ventricle (indicated by the blue
arrow) and external capsule tract (indicated by the red arrow), the
artifacts introduced by upsampling methods are visible on strong
edges, but these artifacts are not present when using the proposed
method. Compared with the non-local upsampling method (Fig. 7C), the proposed method (Fig. 7D and E) preserved greater details
along association tracts (indicated by the green arrow). The
qualitative performance of proposed-5 grad (Fig. 7D) and proposed-RI-5 grad (Fig. 7E) is somewhat similar, however, this
is likely due to the tolerance of the DTI reconstruction method to
small quantitative differences (Fig.
2). Fig. 8 presents the
principal eigenvector of the tensor around the corpus callosum for
the gold standard and the compared methods. Although all five
methods maintained tensor orientation of most pixels, some single
fiber tensors in the corpus callosum (the region indicated by the
red box) were smoothed by B-spline interpolation (Fig. 8C) and non-local upsampling (Fig. 8D), whereas this did not appear with
the proposed method (Fig. 8E and F).
In addition, the proposed method achieved sharper interpolation
than the other methods in the fiber crossing area from the corpus
callosum to the ventricle.
 | Table II.PSNR/SSIM values from the fractional
anisotropy map compared between the different methods. |
Table II.
PSNR/SSIM values from the fractional
anisotropy map compared between the different methods.
| Parameter | B-Spline | Non-local | Proposed-5
grad | Proposed-RI-5
grad |
|---|
| PSNR/SSIM | 22.0/0.90 | 22.3/0.91 | 23.3/0.92 | 24.14/0.94 |
Physical phantom results
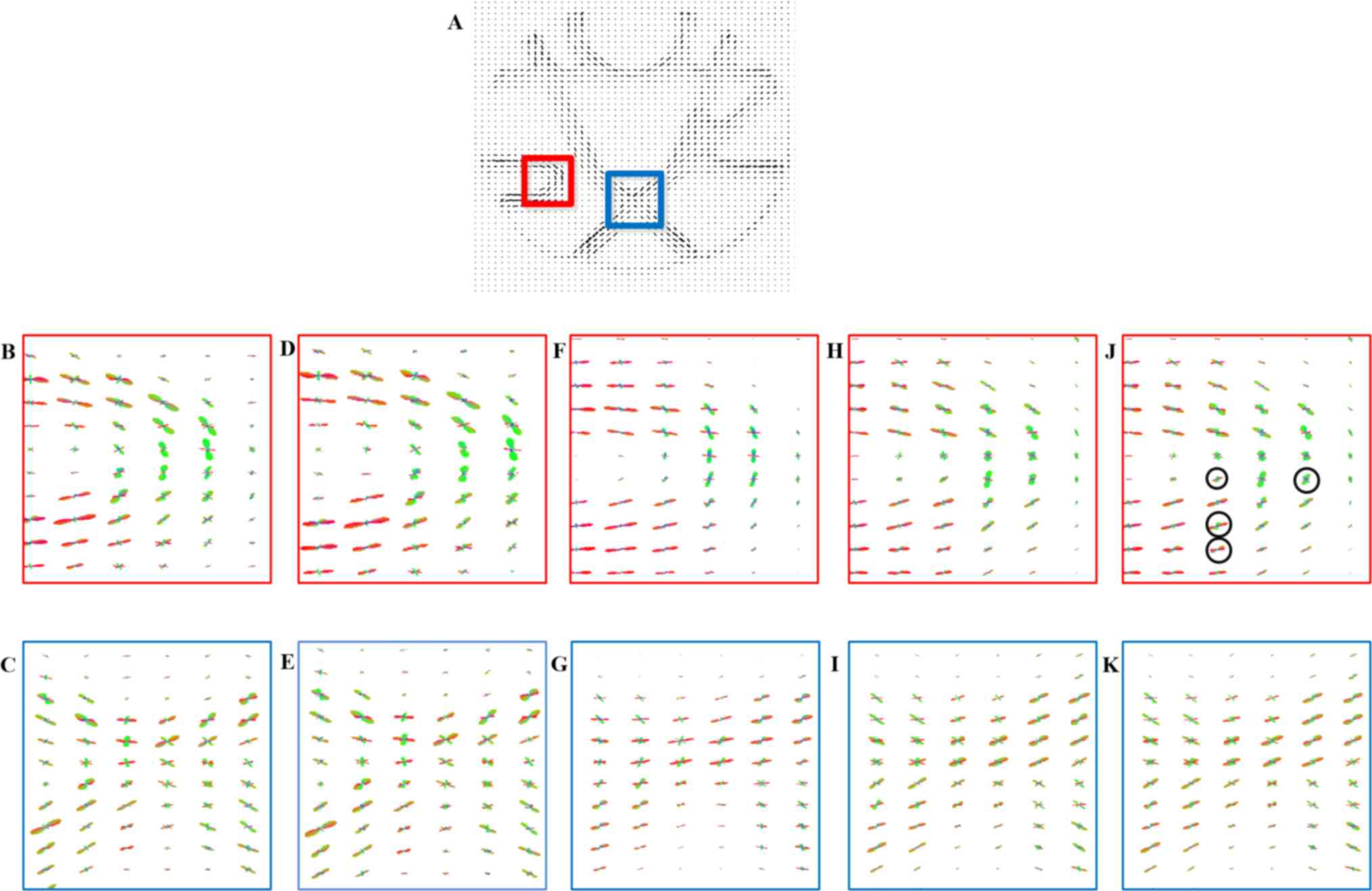
Fig. 9 presents the
ODF obtained by spherical deconvolution for the B-spline, non-local
upsampling, proposed-5 grad and proposed-RI-5 grad methods with the
gold standard used as a reference. For better visualization, the
regions of the sharp turn (second row) and crossing (third row)
were enlarged. The B-spline interpolation was obtained over
smoothed results from which a great deal of ODF information is
missing. As indicated in Fig. 9J and
K, the proposed method better resolves fiber sharp turn and
crossing areas to facilitate fiber tracking. Circles are used to
indicate the differences in performance (Fig. 9J). Close inspections reveal that the
proposed-RI-5 grad better resolved the vertical component, which is
represented by the green lobe of each ODF and with a stronger green
lobe, better tracking of the sharp turn can be achieved.
Discussion
The present study developed a novel SR method based
on a non-local mean filter to increase the spatial resolution of
the DW/I dataset. The proposed method comprised an extension of the
non-local SR method for more accurate HR image reconstruction using
the joint information from adjacent scanning directions.
Furthermore, an efficient rotationally invariant similarity measure
was introduced for further improvement of the reconstruction
together with reduction of computational complexity. The
experimental results demonstrated that the proposed method not only
improved the spatial resolution of DWI in a qualitative and
quantitative manner, but also improved the estimation of diffusion
parameters in DTI and HARDI.
First, the impact of the DWI direction numbers
involved in the reconstruction was studied. Quantitative and
qualitative experimental results demonstrated that the involvement
of similarity redundancy in the nearby directions, namely joint
information, allowed for a more accurate reconstruction of the DWI
dataset. This is probably due to the fact that through the use of
joint information, intrinsic information was retrieved from
adjacent DWI channels, which is beneficial for more detailed
reconstruction in the HR images. However, the increase of direction
numbers is not unlimited and in the present experiment, using >5
directions did not improve the results in any notable way. This may
be attributed to the fact that a similarity comparison used for the
non-local super-resolution was not efficiently improved through
increasing the DWI images involved, which is also in accordance
with previous denoising results (16).
The impact of diffusion parameter estimations was
then compared. As mentioned above, the use of joint information
improved the accuracy of diffusion parameter estimations using the
DTI and the HARDI model, which may be beneficial for further
clinical applications to image the brain in more detail. In
comparison, the HARDI model is more beneficial in this framework.
As indicated in Fig. 9, the
estimated ODF using spherical deconvolution (33) has a more distinct geometric structure
in the complex region, including crossing and sharp corners. Since
the ODF estimation in a complex region remains an open problem for
investigation, super-resolution using joint information may
resemble a supplementary methodology for studies in the field.
In addition, compared with most conventional
interpolation algorithms, which process each DWI component
independently, the proposed method achieved notably higher-quality
results, which can be contributed to two main features. Firstly,
conventional interpolation techniques tend to increase the
smoothness of the images, while the proposed non-local based
reconstruction is highly anisotropic due to similar voxels being
involved in averaging operations (12), yielding greater sharpness in the
results. Secondly, a combination of all the DWI data reveals
complex structures in the white matter. A significant amount of
information redundancy between adjacent directions is utilized to
fit the reconstruction of the white matter bundle (Figs. 6 and 7). Although the improvement is not so
evident in qualitative observations from the in vivo
experiments, the evaluation presented in Table II suggests that quantitative DTI may
benefit from the joint information approaches.
Furthermore, compared with another intermodality
method implemented previously (23),
the method of the present study does not require any registration
steps, since only the DWI dataset is required. This avoids bias
introduced by registration and other modality images.
Finally, Computational complexity is another
important issue for non-local based SR methods as well as DWI
processing. For a typical DWI dataset with a matrix size of
128×128, 60 slices and 32 directions, the runtime for a single
direction was ~8 min for non-local upsampling, 30 min for the
proposed-5 grad, and 10 min for the proposed-RI-5 grad. It is
expected that the implementation of parallel computing on a graphic
processing unit may further speed up the reconstruction and
therefore further studies focusing on this are required.
In conclusion, the present study proposed a single
image non-local SR method for a DWI dataset. Compared with
currently used methods, the proposed framework introduced joint
information to improve the weighting scheme yet with a better image
reconstruction. Furthermore, the reconstruction of the HR image was
further improved by introducing a rotationally invariant similarity
measure to ensure a more accurate regularization procedure in SR
and effectively reduce the computational burden. Experimentation
using a synthetic as well as a real DWI dataset demonstrated that
the proposed method achieved better reconstruction of detailed
information in DWI and more accurate estimations of diffusion
parameters from DTI and HARDI models. In addition, the present
method did not require any extra data acquisition or preprocessing
procedures, and may potentially improve on other super-resolution
algorithms.
Acknowledgements
The present study was supported by a program of the
Sichuan Science & Technology Foundation (grant no. 2017RZ0012)
and a program of the National Natural Science Foundation of China
(grant no. 61303126). Part of the results published in this study
were previously presented at the 2015 Institute of Electrical and
Electronics Engineers International Conference on Digital Signal
Processing on 21–24 July 2015 in Singapore (17).
References
|
1
|
Johansen-Berg H and Behrens T: Diffusion
MRI. Academic Press; New York, NY, USA: 2nd. 2013
|
|
2
|
Peled S and Yeshurun Y: Superresolution in
MRI: Application to human white matter fiber tract visualization by
diffusion tensor imaging. Magn Reson Med. 45:29–35. 2001.
View Article : Google Scholar : PubMed/NCBI
|
|
3
|
Alexander AL, Hasan KM, Lazar M, Tsuruda
JS and Parker DL: Analysis of partial volume effects in
diffusion-tensor MRI. Magn Reson Med. 45:770–780. 2001. View Article : Google Scholar : PubMed/NCBI
|
|
4
|
Mori S and van Zijl PC: Fiber tracking:
Principles and strategies - a technical review. NMR Biomed.
15:468–480. 2002. View Article : Google Scholar : PubMed/NCBI
|
|
5
|
Miller KL, Stagg CJ, Douaud G, Jbabdi S,
Smith SM, Behrens TE, Jenkinson M, Chance SA, Esiri MM, Voets NL,
et al: Diffusion imaging of whole, post-mortem human brains on a
clinical MRI scanner. Neuroimage. 57:167–181. 2011. View Article : Google Scholar : PubMed/NCBI
|
|
6
|
Hu X and Norris DG: Advances in high-field
magnetic resonance imaging. Annu Rev Biomed Eng. 6:1572004.
View Article : Google Scholar : PubMed/NCBI
|
|
7
|
Kimmlingen R, Eberlein E, Gebhardt M,
Hartinger B, Ladebeck R, Lazar R, Reese T, Riegler J, Schmitt F,
Sorensen GA, et al: An easy to exchange high performance head
gradient insert for a 3T whole body MRI system: First results. Proc
Intl Soc Mag Reson Med. 11:pp. 16302004;
|
|
8
|
Scherrer B, Gholipour A and Warfield SK:
Super-resolution reconstruction to increase the spatial resolution
of diffusion weighted images from orthogonal anisotropic
acquisitions. Med Image Anal. 16:1465–1476. 2012. View Article : Google Scholar : PubMed/NCBI
|
|
9
|
Irani M and Peleg S: Motion analysis for
image enhancement: Resolution, occlusion and transparency. J Vis
Commun Image R. 4:324–335. 1993. View Article : Google Scholar
|
|
10
|
Arsigny V, Fillard P, Pennec X and Ayache
N: Log-Euclidean metrics for fast and simple calculus on diffusion
tensors. Magn Reson Med. 56:411–421. 2006. View Article : Google Scholar : PubMed/NCBI
|
|
11
|
Calamante F, Tournier JD, Jackson GD and
Connelly A: Track-density imaging (TDI): Super-resolution white
matter imaging using whole-brain track-density mapping. Neuroimage.
53:1233–1243. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
12
|
Manjón JV, Coupé P, Buades A, Fonov V,
Collins D Louis and Robles M: Non-local MRI upsampling. Med Image
Anal. 14:784–792. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
13
|
Rueda A, Malpica N and Romero E:
Single-image super-resolution of brain MR images using overcomplete
dictionaries. Med Image Anal. 17:113–132. 2013. View Article : Google Scholar : PubMed/NCBI
|
|
14
|
Fillard P, Pennec X, Arsigny V and Ayache
N: Clinical DT-MRI estimation, smoothing and fiber tracking with
log-euclidean metrics. IEEE Trans Med Imaging. 26:1472–1482. 2007.
View Article : Google Scholar : PubMed/NCBI
|
|
15
|
Tristán-Vega A, Westin CF and
Aja-Fernández S: A new methodology for the estimation of fiber
populations in the white matter of the brain with the Funk-Radon
transform. Neuroimage. 49:1301–1315. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
16
|
Tristán-Vega A and Aja-Fernández S: DWI
filtering using joint information for DTI and HARDI. Med Image
Anal. 14:205–218. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
17
|
Yang Z and He P: Non-local diffusion
weighted image super-resolution using collaborative joint
information. Digital Signal Processing (DSP) IEEE. 1–273. 2015.
|
|
18
|
Buades A, Coll B and Morel JM: A non-local
algorithm for image denoising. Computer Vision and Pattern
Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on.
2005; View Article : Google Scholar
|
|
19
|
Manjón JV, Coupé P, Buades A, Collins D
Louis and Robles M: New methods for MRI denoising based on
sparseness and self-similarity. Med Image Anal. 16:18–27. 2012.
View Article : Google Scholar : PubMed/NCBI
|
|
20
|
Lou Y, Favaro P, Soatto S and Bertozzi A:
Nonlocal similarity image filtering. In Image Analysis and
Processing - ICIAP 2009–15th International Conference, Proceedings.
5716:pp. 62–71. 2009; View Article : Google Scholar
|
|
21
|
Wu X, Liu S, Wu M, Sun H, Zhou J, Gong Q
and Ding Z: Nonlocal denoising using anisotropic structure tensor
for 3D MRI. Med Phys. 40:1019042013. View Article : Google Scholar : PubMed/NCBI
|
|
22
|
Rousseau F: Brain hallucination. Computer
Vision-ECCV. 5302:497–508. 2008.
|
|
23
|
Rousseau F: Alzheimer's Disease
Neuroimaging Initiative: A non-local approach for image
super-resolution using intermodality priors. Med Image Anal.
14:594–605. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
24
|
Coupé P, Manjón JV, Chamberland M,
Descoteaux M and Hiba B: Collaborative patch-based super-resolution
for diffusion-weighted images. Neuroimage. 83:245–261. 2013.
View Article : Google Scholar : PubMed/NCBI
|
|
25
|
Banerjee J and Jawahar CV:
Super-resolution of text images using edge-directed tangent field.
DAS. 76–83. 2008.
|
|
26
|
Tournier JD, Calamante F and Connelly A:
MRtrix: Diffusion tractography in crossing fiber regions. Int J
Imaging Syst Technol. 22:53–66. 2012. View Article : Google Scholar
|
|
27
|
Raffelt D, Tournier JD, Rose S, Ridgway
GR, Henderson R, Crozier S, Salvado O and Connelly A: Apparent
fibre density: A novel measure for the analysis of
diffusion-weighted magnetic resonance images. Neuroimage.
59:3976–3994. 2012. View Article : Google Scholar : PubMed/NCBI
|
|
28
|
Daducci A, Canales-Rodríguez EJ,
Descoteaux M, Garyfallidis E, Gur Y, Lin YC, Mani M, Merlet S,
Paquette M, Ramirez-Manzanares A, et al: Quantitative comparison of
reconstruction methods for intra-voxel fiber recovery from
diffusion MRI. IEEE Trans Med Imaging. 33:384–399. 2014. View Article : Google Scholar : PubMed/NCBI
|
|
29
|
Wang Z, Bovik AC, Sheikh HR and Simoncelli
EP: Image quality assessment: From error visibility to structural
similarity. IEEE Trans on Image Process. 13:600–612. 2004.
View Article : Google Scholar
|
|
30
|
Fillard P, Descoteaux M, Goh A, Gouttard
S, Jeurissen B, Malcolm J, Ramirez-Manzanares A, Reisert M, Sakaie
K, Tensaouti F, et al: Quantitative evaluation of 10 tractography
algorithms on a realistic diffusion MR phantom. Neuroimage.
56:220–234. 2011. View Article : Google Scholar : PubMed/NCBI
|
|
31
|
Poupon C, Rieul B, Kezele I, Perrin M,
Poupon F and Mangin JF: New diffusion phantoms dedicated to the
study and validation of high-angular resolution diffusion imaging
(HARDI) models. Magn Reson Med. 60:1276–1283. 2008. View Article : Google Scholar : PubMed/NCBI
|
|
32
|
Basser PJ, Matiello J and Bihan DL:
Estimation of the effective self-diffusion tensor from the NMR spin
echo. J Magn Reson B. 103:247–254. 1994. View Article : Google Scholar : PubMed/NCBI
|
|
33
|
Tournier JD, Calamante F and Connelly A:
Robust determination of the fibre orientation distribution in
diffusion MRI: Non-negativity constrained super-resolved spherical
deconvolution. Neuroimage. 35:1459–1472. 2007. View Article : Google Scholar : PubMed/NCBI
|
|
34
|
Basser PJ, Mattielo J and LeBihan D:
Estimation of the effective self-diffusion tensor from the NMR spin
echo. J Magn Reson B. 103:247–254. 1994. View Article : Google Scholar : PubMed/NCBI
|
|
35
|
Smith SM, Jenkinson M, Woolrich MW,
Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M,
Drobnjak I, Flitney DE, et al: Advances in functional and
structural MR image analysis and implementation as FSL. Neuroimage.
23 Suppl 1:S208–S219. 1994. View Article : Google Scholar
|