This article is mentioned in:

Introduction

Osteoporosis (OP) has become a major public health problem in the ageing population. As the thoracolumbar spine is the transitional site of the fixed thoracic (T) spine to active lumbar (L) spine (T11-L2), it is biomechanically vulnerable to injury (1,2). Low-energy injuries, such as falls, can cause compression fractures of the thoracolumbar junction in patients with OP (2,3). For some patients, bed rest is required after a fracture due to surgical contraindications, such as high blood pressure or severe coronary heart disease; however, this may lead to long-term lower back pain and discomfort, kyphosis of the spine and a decline in quality of life (2). The medical and economic costs of osteoporotic compression fractures are rapidly increasing (4,5). Hence, the accurate assessment of local stress in the thoracolumbar junction during a backward fall is important in further understanding the injury mechanism and may provide a reference for the future study of protective devices. However, due to the position of the thoracolumbar spine, it is difficult to directly measure the force condition during the backward fall process (6,7). Nevertheless, finite element (FE) analysis (FEA) has made a significant contribution to the research and understanding of spinal mechanics. The effectiveness of spinal FEA has been confirmed in previous studies (8,9). During FEA, 3D-irregular geometry is constructed, and the non-uniform materials are arranged. Next, large complex loads and motions are applied, and the contact of facet joints is simulated (10). However, due to the inherent defects of FEA, such as a large accuracy floating, the results of FE simulation must be fully validated to ensure the accuracy compared with the real-life situation (11). Hence, analysis of direct FE validation was used in the present study to ensure the accuracy of results based on an experimental test and the relative FE simulation.

In the present study, the body posture and hip contact force values in the falling process were obtained using a human body backward fall simulation experiment. The hip contact force and the direction measured were then used as loading conditions. These were directly given to a human body trunk FE model for quasi-static FE simulation, in order to accurately obtain the structures of the thoracolumbar junction involved in the backward fall process. The stress condition and stress concentration were then used to evaluate the injury mechanism of the local area in the process of a backward fall.

Materials and methods

Volunteer information

A healthy young man (age, 24 years; height, 172 cm; weight, 70 kg), with no past medical history of bone tumors and fractures, OP or concussion, was recruited. The current study was approved by the Ethics Committee of Jiangxi Provincial People's Hospital Affiliated to Nanchang University (Nanjing, China), and written informed consent was provided by the volunteer.

Biomechanical test of a backward fall

A 3D force table (BP400600; Advanced Mechanical Technology, Inc.) was used to record the hip force during the backward fall process. During the test, in order to protect the volunteer, a 5 cm-thick high-density sponge with a density of 45 kg/m3 was laid above the force table. The size of the sponge was 60x40x5 cm3, which was required to cover the surface but not exceed the edge of the platform (6). In addition, the volunteer kept their body straight, at an angle of 30˚ to the vertical axis, and held a fixed rope that could be released at will. When the described initial state was maintained by the volunteer, the rope was released suddenly under the condition of diverting the volunteer's attention, so as to achieve the state of simulated unprepared backward fall (Fig. 1). Data acquisition frequency of the force platform was set as 50 Hz, and the precision was 0.01 N. The backward fall was mimicked at least three times and the impact force on the hip was collected each time. The average impact force was then calculated.

Figure 1 Schematic diagram of the backward fall experiment. All figures should be interpretable with just the figure itself and its corresponding figure legend; without having to refer back to the main text of the manuscript, similarly hereinafter.

FEA

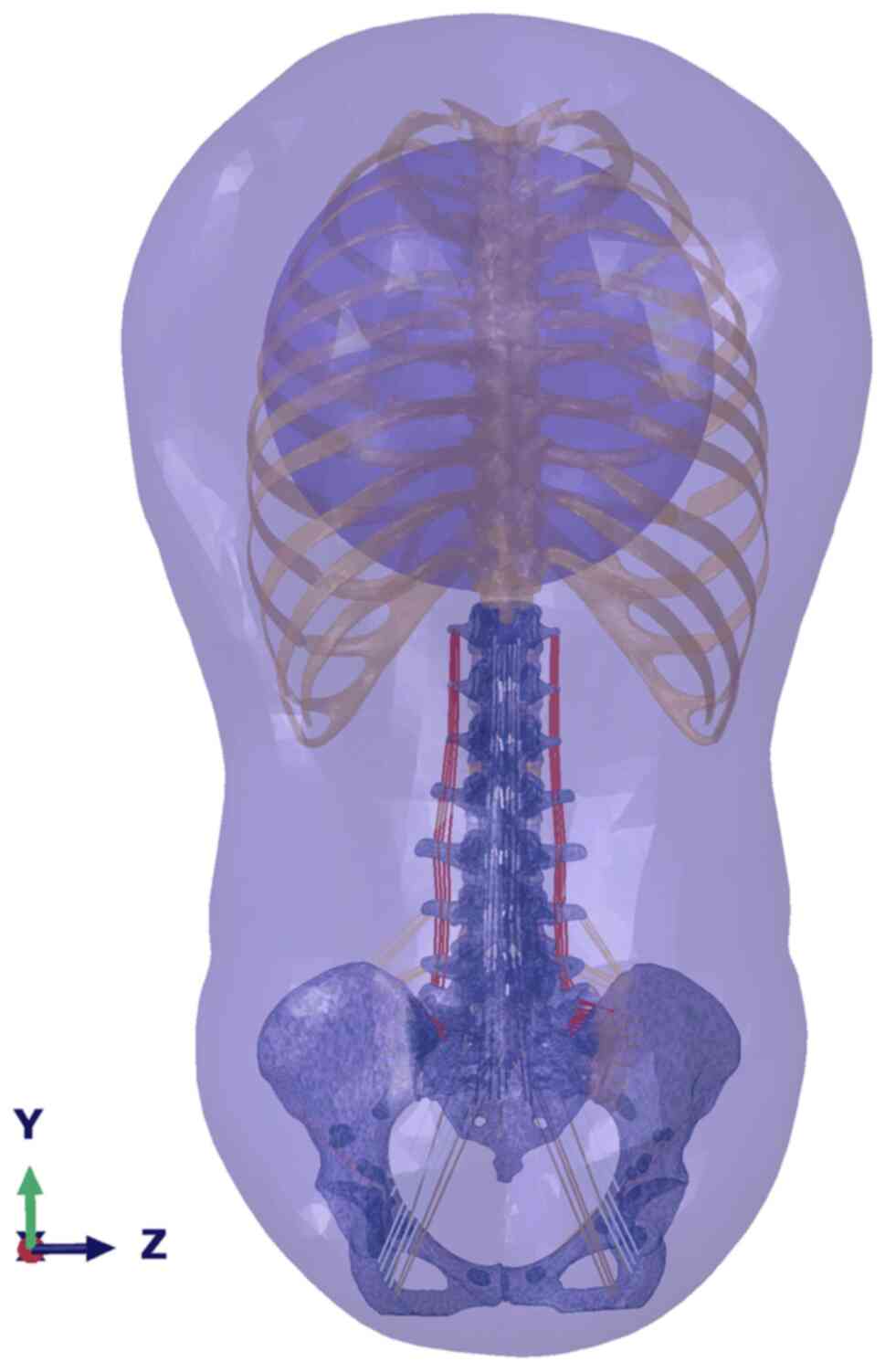
Abaqus 2016 software (Dassault Systèmes) was used to simulate the stress state of the human trunk during the process of backward fall (Fig. 2) (12). Firstly, computed tomography (CT) scan data of the volunteer were collected from a dual-source 64-slice spiral CT system (Siemens AG) at Jiangxi Provincial People's Hospital Affiliated to Nanchang University. The scan parameters were set as 120 kV voltage and 0.625 mm pitch. All original CT data were stored in digital imaging communications in medicine format, and then imported into Mimics 19.0 software (Materialise NV) for reconstruction. The 3D models of overall trunk surface, vertebrae, thorax and the pelvis were separately divided and saved in stereolithography (STL) format.

Figure 2 Finite element simulation of the backward fall experiment.

The 3D models in STL format were imported into Geomagic 2016 software (3D Systems, Inc.) to be modified and exported as IGES format models. These were then imported into Hypermesh 14.0 software (Altair Engineering, Inc.) for further Boolean operation, meshing, addition of truss unit ligament structures and the endowment of each structure with validated material property parameters, to establish the final FE model of the trunk.

The linear and isotropic elasticity property of the FE model was developed, which included cortical and trabecular bone, ligament and cartilage structures, intervertebral disc and surrounding soft tissues. During the mesh procedure, seed sizes were set to 1-3 mm, and a finer mesh size was used for the regions of interest of the thoracolumbar junction, including T11, T12 and the upper lumbar region. An almost 0.5-mm gap was used for the facet joint of lumbar vertebrae, but the non-contact condition (within the torque of 7.5 N·m) was defined to avoid nonconvergence and decrease the expense of the FEA simulation.

The FE model was then imported into Abaqus software to set the boundary conditions and load accurate force-time parameters of the sacrococcygeal bony structures obtained using the Anybody software (Anybody Technology AS) simulation calculation. The upper thoracic margin was set as a fixed boundary condition, the loading point was set as the ischial tubercle and the loading was carried out step-by-step according to the force-time curve. The material properties and node information of bony and soft-tissue structures in the FE model are shown in Table I, and material attribute parameters of each ligament are shown in Table II. Moreover, all FE models were simulated based on quasi-static analysis by Abaqus/standard solver on a T7900 tower workstation (Dell Inc.). Regarding the AVG 75%, if the AVG was set to 1, it meant that the stress calculation of all nodes in the display area were used for generating the average; therefore, a smoother cloud image was created. If AVG was set to 75%, it meant that when the relative node variable was less than the value and the result of the node was averaged.

Table I Material properties of bony and soft-tissue structures of finite element analysis model.

Table I

Material properties of bony and soft-tissue structures of finite element analysis model.

First author (year)	Structure	Elasticity modulus E (MPa)	Poisson's ratio (υ)	Number of elements	Number of nodes	Type of element	(Refs.)
Denozière and Ku (2006), El-Rich et al (2009) and Moramarco et al (2010)	Cortical bone	12,000	0.3	756,474	217,388	C3D4	(31-33)
El-Rich et al (2009) and Moramarco et al (2010)	Cancellous bone	100	0.2	127,110	34,110	C3D4	(31,32)
Denozière and Ku (2006), El-Rich et al (2009), Moramarco et al (2010) and Guo and Li (2020)	Fiber ring	450	0.3	75,790	22,104	C3D4	(31-34)
Denozière and Ku (2006) and El-Rich et al (2009)	Nucleus pulposus	1	0.5	35,510	10,100	C3D4	(31,32)
Denozière and Ku (2006), Moramarco et al (2010) and Guo and Li (2020)	Cartilage	23.8	0.4	2,622	859	C3D4	(31,33,34)
Moramarco et al (2010) and Guo and Li (2020)	Soft tissue	1.5	0.4	503,217	112,249	C3D4	(33,34)

Table II Material properties of ligament tissues.

Table II

Material properties of ligament tissues.

First author (year)	Ligament tissue	Elasticity modulus E (Mpa)	Poisson's ratio (υ)	Transverse area (mm2)	Number of elements	Type of element	(Refs.)
Guo and Li (2020) and Kong and Goel (2003)	Anterior longitudinal ligament	7.8	0.3	24	42	Truss (T3D2)	(34,35)
Guo and Li (2020) and Kong and Goel (2003)	Posterior longitudinal ligament	10	0.3	14.4	42	Truss (T3D2)	(34,35)
Guo and Li (2020) and Kong et al (2003) flavum	Ligamentum	15	0.3	40	36	Truss (T3D2)	(34,35)
Guo and Li (2020) and Kong et al (2003)	Supraspinous ligament	8	0.3	23	7	Truss (T3D2)	(34,35)
Guo and Li (2020)	Interspinous ligaments	10	0.3	26	28	Truss (T3D2)	(34)
Guo and Li (2020)	Intertransverse ligament	10	0.3	3.6	56	Truss (T3D2)	(34)
Guo and Li (2020)	Iliolumbar ligament	75	0.3	25	12	Truss (T3D2)	(34)
Guo and Li (2020)	Sacrospinous ligament	12.6	0.2	25	8	Truss (T3D2)	(34)
Guo and Li (2020)	Sacrotuberous ligament	33	0.3	539	8	Truss (T3D2)	(34)
Guo and Li (2020)	Inguinal ligament	2.6	0.3	45	6	Truss (T3D2)	(34)
Kong and Goel (2003)	Anterior sacroiliac ligaments	208	0.2	25	20	Truss (T3D2)	(35)
Kong and Goel (2003)	Posterior sacroiliac ligament	133	0.2	25	20	Truss (T3D2)	(35)

At FEA simulation data collection, 50 representative nodes in the stress concentration part of the thoracolumbar spine were selected to calculate the average von Mises stress value as the overall stress value of the structure.

Results

Backward fall experiment

The results of the backward fall experiment showed that the sacrococcygeal region of the volunteer landed first, and that the hip joint was at a state of flexion at this time. During the process of backward fall, the trunk was flexed at the time of landing, and the trunk was extended after landing. The total impact time of landing was 1.14±0.58 sec, and the maximum impact force was 4,056±263 N, which is approximately six-times the body weight of the volunteer.

FE simulation of a backward fall

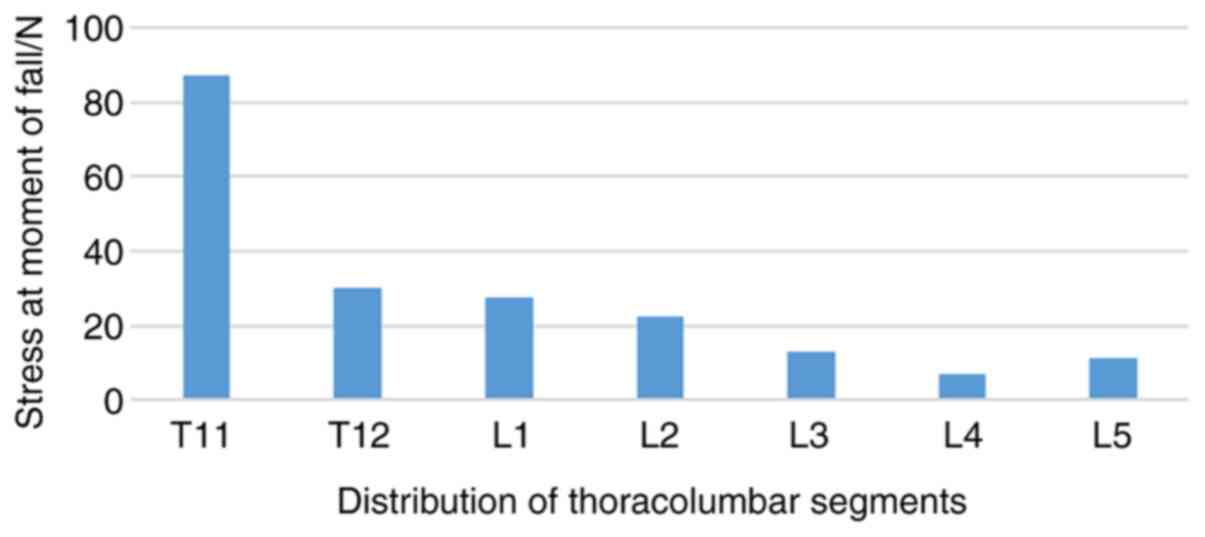
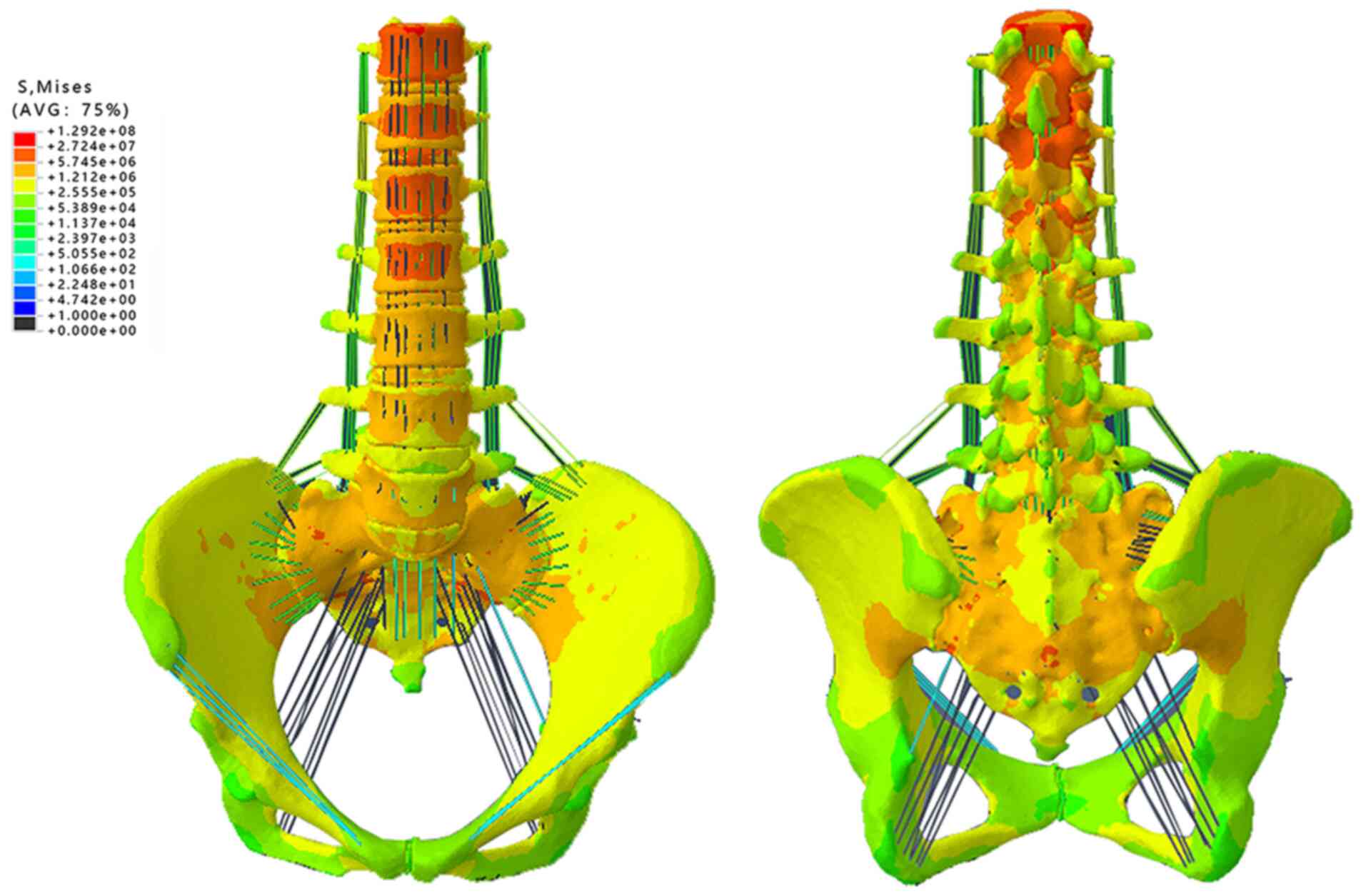
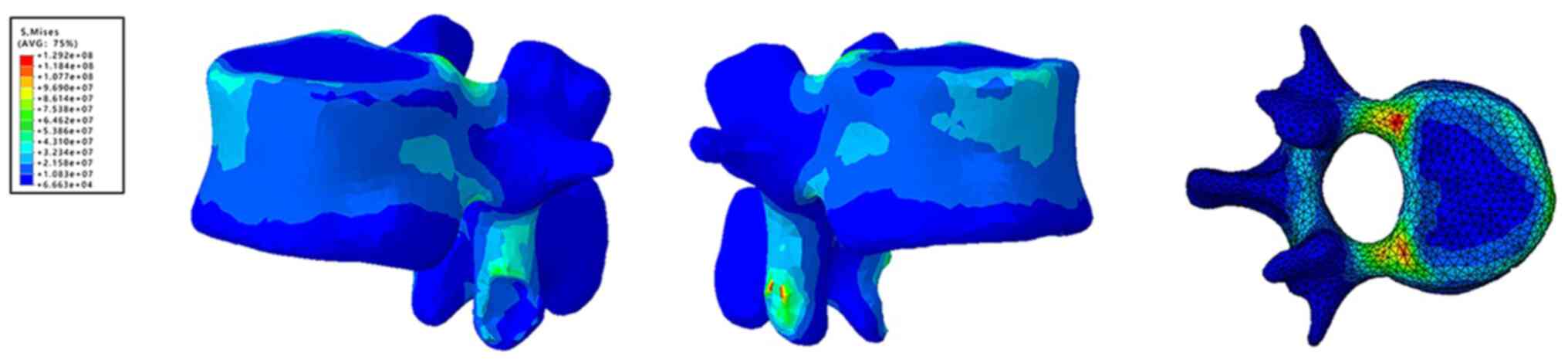
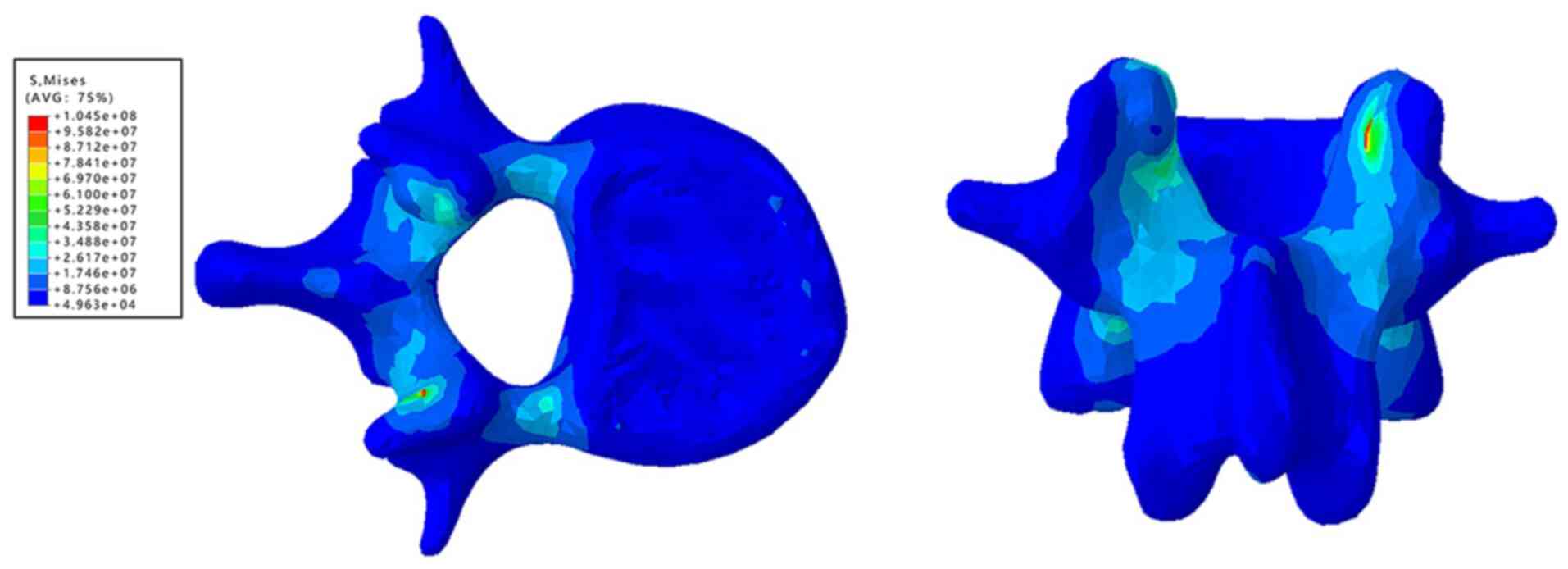
Under static loading, the stress of each vertebral structure decreased gradually along the spine, following the peak value of stress, which appeared at 0.4 sec (Fig. 3), and the stress of the T11 front vertebral body was as high as 42 MPa (Fig. 4). In addition, the stress of the T11 rear edge and pedicle junction was as high as 70.67 MPa (Fig. 5), and the maximum stress value between the inferior articular process and upper articular process of T12 was ~128 MPa (Fig. 6). 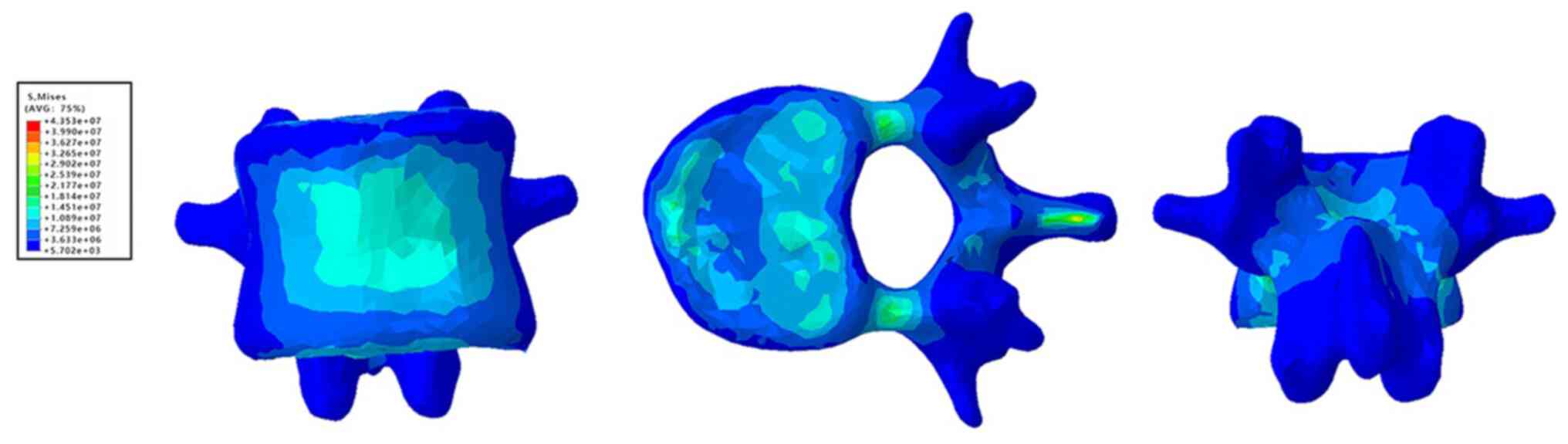Moreover, the average stress of T12 and the front edge of L1 was 25 MPa, and the maximum stress of the end plate was 21.7 MPa, which was mainly distributed in the central and posterior part of the end plate and surrounding cortex (Figs. 6 and 7).

Figure 3 Stress distribution of each segment during the process of a backward fall.

Figure 4 Stress nephogram of thoracolumbar vertebrae in falling state. S was the stress value in each direction, Mises was von Mises stress. Avg 75% was the default averaging threshold, which was used to average variables (the same below). S, stress value; Mises, von Mises stress; AVG, default averaging threshold.

Figure 5 Stress nephogram of T11. The stress concentration at the front of the vertebral body, the junction of the pedicle and vertebral body and the lower joint was found at varying degrees, and the highest stress was found at the process of the lower joint. S, stress value; Mises, von Mises stress; AVG, default averaging threshold.

Figure 6 Stress nephogram of T12. There was a demonstratable stress concentration at the front of the vertebral body and pedicle. The stress at the cancellous bone area of endplate was greater than that at the cortical bone area, and the highest stress was found at the superior articular process. S, stress value; Mises, von Mises stress; AVG, default averaging threshold.

Figure 7 Stress nephogram of L1. There was a clear stress concentration at the end plate of the vertebral body, and the highest stress region of pedicle was close to that of T11 and T12. S, stress value; Mises, von Mises stress; AVG, default averaging threshold.

Discussion

Thoracolumbar vertebral compression fractures caused by OP are a common and difficult problem faced by spinal surgeons, with the majority of patients being elderly (13). The direct cause of fractures is that the load acting on the vertebral body causes an internal stress which exceeds the mechanical strength of the vertebra. Therefore, regardless of bone condition, the vertebral body load is critical for the formation of fractures (14,15). Previous fall experiments have mainly focused on the instantaneous posture of various parts of the body during the process of a backward fall (16,17), while the impact force of a backward fall has not been as well studied. Only the instantaneous posture and the force value of the force point can be measured using force-measuring platforms. This means that the mechanical mechanism of strength transmission to the spine leading to spinal fracture after a backward fall cannot be accurately determined (18,19).

Khalili et al (20) previously designed an inverted pendulum model, in which the pine was defined as a single straight rod. However, this model makes it difficult to directly obtain the stress condition of the column section during the process of a backward fall. As an effective way of performing a spinal mechanics experiment, the FE model can effectively predict the strength of spinal bone, fracture sites and stress distribution (11). However, most FE studies of fall experiments have involved simulating stress on the hip (21,22), and these experimental FE models were not able to simulate the human postures involved in the process of a backward fall, which impacted on the results. Similarly, in the process of thoracolumbar segments during injury, most of the FE research methods were performed using axial impact (10). In the setting of loading conditions, due to various reasons such as limited conditions, the stress situation of subjects was not able to be added accurately. Hence, in the present study, a healthy male volunteer participated in simulating a real-life fall before a simulated fall spine stress FE experiment was carried out to obtain the accurate fall data. This provided reliable data for further understanding of the stress mechanism of the spinal structures during the backward fall process.

In order to obtain accurate fall data, this experiment simulated the real-life backward fall process. Therein, it was found that at the moment of impact, the subject was in a flexion state with the hip joint, the sacrococcygeal region landed first, then the hip joint extended, and the chest, waist and back were stressed. The results were consistent with the fall experiment postures shown by Li et al (23) and Khalili et al (20), and the hip impact force reached 4,056±253 N.

For validation of the FE model, there are few prior FE studies that simulate the backward fall process to measure the stress on the spine. In the present study, an FE model was generated based on the experimental data of a backward fall, in order to analyze the stress mechanism of each segment of the thoracolumbar spine during this process. In previous studies, it was hypothesized that compression fractures accounted for the vast majority of thoracolumbar fractures caused by falls (20,23). In the FE results of the present study, the stress concentration appeared in the anterior and posterior edge of T11, T12 and L1 vertebrae, upper and lower endplates, pedicle and laminae, and the peak stress appeared in the thoracolumbar segment. This was consistent with results of Gertzbein et al (24) and Nakashima et al (25) after applying axial load to the established FE model. The results of the present study complement those of Qiu et al (26), in which the established FE model of T12 and L1 segments were measured under vertical impact load. In the current study, the high stress areas of the upper and lower endplates were in the nucleus pulposus center and were parallel to each other, and the stress center of cancellous bone was largest near the endplate. The stress of cortical bone was concentrated in the anterior and posterior lower edge of the T12 vertebral body, and anterior and posterior upper edge of the L1 vertebral body. These observations were consistent with the results of lumbar FE demonstrated by Cao et al (14), which found that >50% of vertebral body fractures occur between upper and lower endplates.

It is important to note that there was a clear stress concentration in the joint process of the lower T11, upper T12 and upper L1, as well as the transitional part of the pedicle, and that the stress extended to the posterior edge of the vertebral body through the pedicle. In addition, some studies have hypothesized that the interaction of articular processes causes the increase of stress and the transfer of stress along the pedicle to the vertebral body, resulting in the local stress concentration at the posterior edge of the vertebral body (27,28). Moreover, Wagnac et al (29) reported that when the load of the facet was high at the level of L1-L2, the stress concentration of the pedicle root of this segment also increased, further supporting this hypothesis. In addition, Fradet et al (30) hypothesized that fractures of the pedicle could be caused by multiple loading conditions, such as forward and backward shear combined with flexion, traction combined with flexion, or traction combined with flexion and shear. Hence, it was hypothesized in the present study that the probability of fracture in these stress areas may be increased. Furthermore, by comparing the stress of different vertebrae, it has previously been found that the stress of the L4 vertebrae was significantly lower than that of the surrounding vertebrae when falling backward (30). Combined with the stress process, Gertzbein et al (24) hypothesized that the physiological curvature of vertebrae might lead to the dispersion of conduction force, resulting in the uneven distribution of vertebral force. Hence, it could be inferred from the FE results, that the risk of fracture is increased at the front vertebral body, and the upper and lower endplates of T11-L2 vertebrae after falling backward, and that fractures may occur due to the compression of the front of the vertebrae. Due to the power transmission of the upper and lower articular processes, there is also the risk of fracture at the junction of the pedicle and vertebrae of T12 and L1.

The stress distribution of thoracolumbar junction obtained in the present study showed the injury risk of this structure during the process of backward fall. Furthermore, the method of FEA combined in vivo experimental data was shown to be effective and accurate in this study. Thus, in future research, the method in the present study could be directly used for researching protective devices to prevent injury to the thoracolumbar junction from a backward fall. In addition, the protective effect and mechanism could be evaluated through an additional series of studies, which could aid in the development, optimization and improvement of protective devices for the thoracolumbar junction in OP.

Indeed, certain limitations in the current study should also be recognized and addressed. Firstly, the stress distribution of the thoracolumbar junction obtained in this study was indirectly obtained by FEA, which could provide a certain amount of error. Secondly, the sample size in this study was small, which will need to be increased for further validation. Thirdly, the current common practice is to select a volunteer of standard weight and CT scan data for modeling and simulation, which may not represent the population.

In conclusion, through the combination of FEA and human body backward fall simulation experiment, the backward fall process and the force condition of the sacrococcygeal region can be accurately obtained. The local stress state of the thoracolumbar junction during the process of a backward fall obtained in FE simulation is consistent with previous research, and there is a greater risk of fracture in the front of the T11-L1 vertebral body, the upper and lower endplates, the junction of the T12 and the L1 pedicle and vertebral body.

Acknowledgements

Not applicable.

Funding

Funding: This work was supported by the National Natural Science Foundation of China (grant nos. 81460346 and 81702160).

Availability of data and materials

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Authors' contributions

PDS, XXZ, YWZ, ZW, XYW, YCW, XLY, HRG, XDL, ZZA, JYH and XPD participated in the data collection, data analysis and data interpretation. PDS, XXZ, YWZ and XPD wrote and edited the manuscript. PDS, XXZ, YWZ and XPD contributed to the critical revision of the manuscript. PDS and XPD confirm the authenticity of all the raw data. All authors read and approved the final manuscript.

Ethics approval and consent to participate

The current study was approved by the Ethics Committee of Jiangxi Provincial People's Hospital Affiliated to Nanchang University. Written informed consent was provided by the involved volunteer.

Patient consent for publication

Written informed consent was obtained from the volunteer for the publication of his relevant data and images.

Competing interests

The authors declare that they have no competing interests.

References