This article is mentioned in:

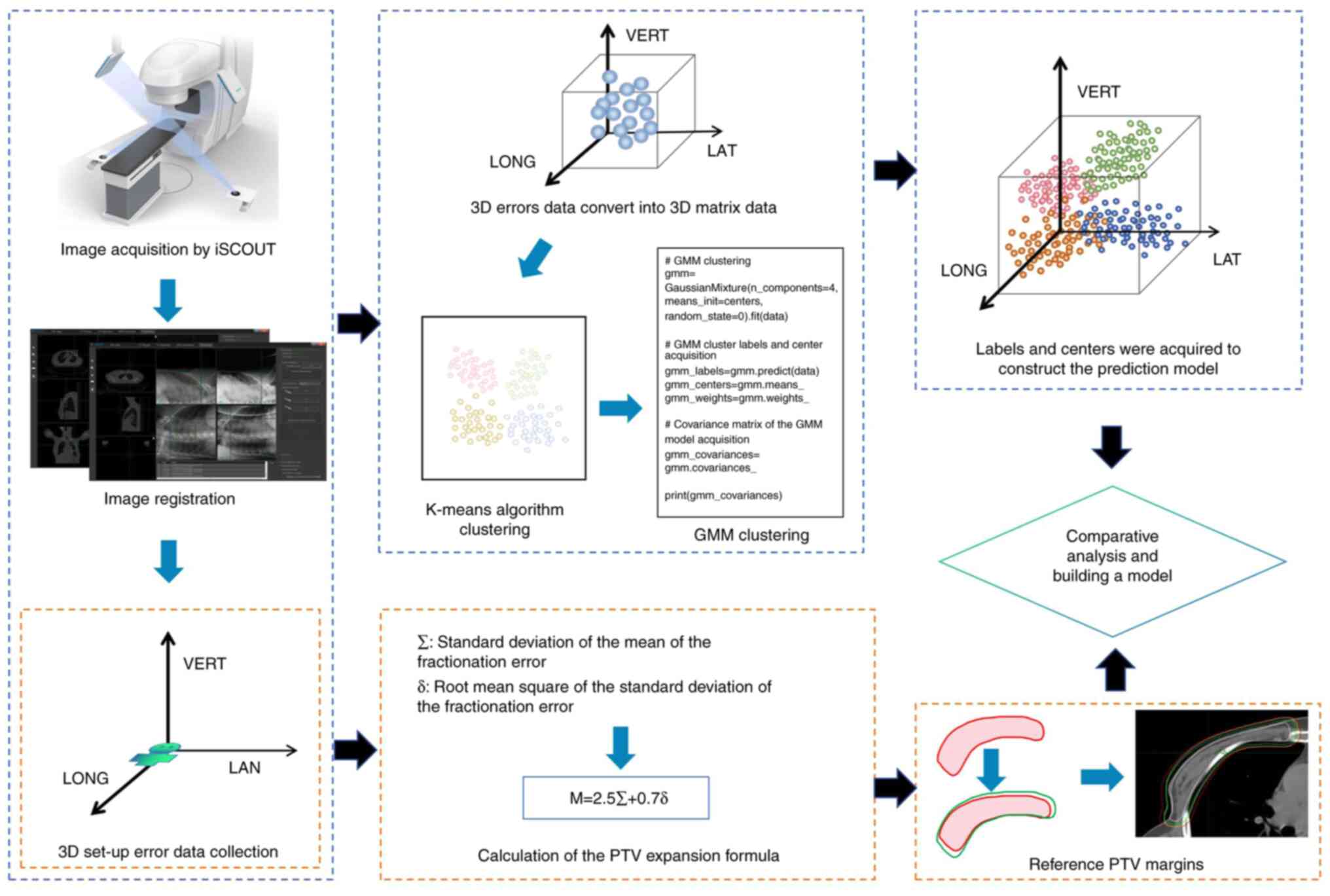
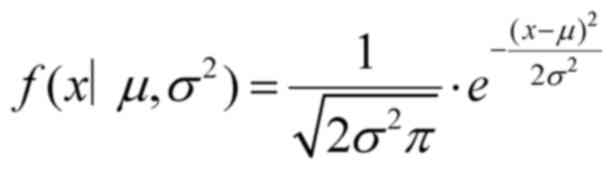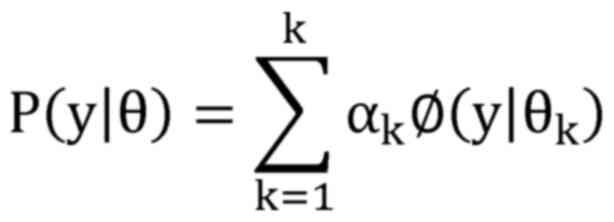Introduction

Breast cancer is the most commonly diagnosed cancer among women worldwide, with ~2.3 million new cases each year (1); it is also a leading cause of cancer-related deaths, responsible for ~670,000 deaths annually (1). Radiotherapy, as an important component of comprehensive breast cancer treatment, is able to effectively extend the survival times of patients with breast cancer (2,3). Set-up errors are the differences between the area in which the patient is actually being treated and the area for which the treatment was planned, for example by registering real-time images with images taken at the time of positioning, usually through an image-guiding device. However, set-up errors during radiotherapy may cause changes in tumor location, leading to dose distribution deviations and affecting treatment efficacy (4). Clinically, image-guided monitoring and the correction of set-up errors are employed to improve the accuracy of radiotherapy. Cone beam computed tomography (CBCT) registration is a traditional image-guided method; however, CBCT involves additional exposure to radiation, which may increase the risk of secondary tumors in patients (5). Therefore, the rational use of image-guided methods or the search for novel methods to obtain and correct set-up errors are important research topics in the field of breast cancer radiotherapy.

Currently, in addition to seeking non-radiative image-guided methods, predicting set-up errors based on past patient data through mathematical modeling or computer deep learning holds notable potential (6,7). The Gaussian Mixture Model (GMM) holds significant advantages in this area, as it is able to both describe complex error distributions and quantify error probabilities (8). Therefore, the aim of the present study was to use GMM to establish a predictive model for the distribution of set-up errors in image-guided radiotherapy (IGRT) for breast cancer. In terms of the results of the present study, the novel aspects of this predictive model are as follows: i) Compared with the traditional image-guided method, the set-up errors obtained via this prediction model aids in avoiding radiation risk; ii) compared with other predictive models such as deep learning, the GMM is simpler, faster and capable of quantitative analysis; and iii) in clinical applications, the GMM facilitates error intervention and correction, reducing set-up errors and improving treatment accuracy.

Patients and methods

Patient selection

In terms of sample size, the empirical method was utilized and the number of patients in previous research literature was assessed; therefore, analysis of >20 patients for the present study was required. The maximum number of patients was collected according to the inclusion and exclusion criteria applied in the study period. The group sample size was then calculated using the power analysis software PASS (version. 15; NCSS, LLC). To collect sufficient data for analysis, 80 patients with breast cancer who were treated in the Department of Radiation Oncology of Fujian Medical University Union Hospital (Fuzhou, China) between January 2021 and January 2022 were selected. The patients were treated using a Varian 23E medical linear accelerator (Varian Medical Systems, Inc.), the radiation dose was 40 Gy/15 fractions and each fraction of the treatment course was image-guided using the iSCOUT® system (version. 1.2.0; Jiangsu Rayer Medical Technology Co., Ltd.). The present study was approved by the Ethics Committee of Fujian Medical University Union Hospital (Fuzhou, China; approval no. 2022WSJK017).

Inclusion and exclusion criteria

To ensure that patients could undergo intensity-modulated radiotherapy and complete the whole course of radiotherapy, the inclusion criteria were as follows: i) Patients who had pathologically confirmed breast cancer; ii) patients who received intensity-modulated radiotherapy following modified radical mastectomy for breast cancer; iii) patients who could raise both arms, fully exposing the affected breast; iv) patients who had a Karnofsky Performance Status score >80; and v) patients who had no other diseases affecting the radiotherapy. The exclusion criteria were as follows: i) Patients who had undergone breast valve surgery; ii) patients who had difficulty supporting their arms and who could not meet the requirements for thermoplastic mask location; and iii) patients who were otherwise unfit or unable to complete the entire study process. Breast cancer was not graded in the present study, which was independent of the study content and results.

Radiotherapy process

Following the standard procedure, all patients were fixed by body bracket with or without thermoplastic film, and scanned using Philips 16-row large-aperture spiral computed tomography (Philips Healthcare), with a slice thickness of 5 mm. The IGRT plan was designed using a Varian Eclipse treatment planning system (version. 15.6; Varian Medical Systems, Inc.). The X-ray energy was 6 MV and the calculation grid was 2.5 mm.

Patients were positioned by two therapists during treatment. Prior to each treatment process, real-time 45 and 135° positioning images were obtained using the iSCOUT system for position verification. The acquired images were automatically registered with the digitally reconstructed images generated at the same angle, performed by a senior therapist using the bone registration mode of the iSCOUT system software. If automatic registration could not obtain the results, manual registration was used. The registration frame was set at the center of the treatment target, and the chest wall, ribs, thoracic vertebrae and clavicle were used as the regions of interest to register the set-up errors in the lateral (LAT), longitudinal (LONG) and vertical (VERT) direction for recording.

Data acquisition and preprocessing

The collected three-dimensional direction data were preprocessed. Each patient underwent 15 sessions of radiotherapy, according to the principle that image guidance should have been performed at least once per session, resulting in 15 sets of three-dimensional data per patient. Any loss of data resulted as a consequence of equipment failures, image quality issues or personal issues of the patients. Patients with >2 sets of missing data were excluded, whereas those with 1–2 sets of missing data had their data completed using the mean value of their existing data to ensure data completeness and authenticity. For each patient, based on clinical error ranges, data with maximum and minimum deviations >15 mm were analyzed, and data from patients with a high degree of variability were excluded to ensure data reasonableness.

Construction of the prediction model

i) From the single Gaussian model to the GMM. The single Gaussian model, also known as the normal distribution, is defined as follows: If a random variable x follows a Gaussian distribution with a mean µ and a variance σ2, it is denoted as N (µ, σ2) (9). The parameter µ represents the mean, which corresponds to the center of the normal distribution, and the parameter σ represents the standard deviation. The probability density function is defined according to the following formula:

The GMM is introduced when the data distribution consists of a linear combination of multiple Gaussian distributions; it can theoretically fit various types of distributions and is usually utilized to deal with data sets containing multiple different distributions. According to the definition, assuming that the data follow the Gaussian mixture distribution, then the probability distribution model has the following formula:

where αk represents the weight coefficient, αk≥0, ∑k=1kαk=1; ø(y|θk) is the Gaussian distribution density, θk=(μk,σkk) and the Gaussian distribution density is as follows: ø(y|θk)=12α2πe(y-μk)22αk2. That is, it represents the k-th Gaussian distribution density function.

ii) Expectation maximization (EM) algorithm. The EM algorithm is used in statistics to find the maximum likelihood estimates of parameters in probabilistic models that depend on unobserved latent variables; it is an effective method for solving optimization problems involving hidden variables. Since the GMM function is difficult to handle through partial derivatives, the EM algorithm is commonly used to solve its parameters. The EM algorithm is iterative, with each iteration consisting of an expectation step and a maximization step.

iii) K-means algorithm. The K-means algorithm is usually used in clustering, and its fundamental principle is that the distance between the points inside the cluster is smaller than the distance between the points outside the cluster (10). The K-means algorithm and the GMM can express each other under certain conditions. The K-means algorithm may be regarded as a special form of the GMM, whereas the GMM provides stronger descriptive power. The GMM is more computationally intensive than the K-means algorithm per iteration. Therefore, usually in practical applications, the K-means algorithm is used to obtain the initial clustering results first, and subsequently, its cluster number and cluster center are passed to the GMM as initial values for a more meticulous iteration.

The implementation of the K-means algorithm comprises the following steps: a) K center points are randomly selected; b) the data are traversed, and each data point is assigned to the nearest center class; c) the mean value of each cluster is then calculated and used as the new center; and d) finally, steps b and c are repeated until either the convergence or the maximum number of iterations is reached.

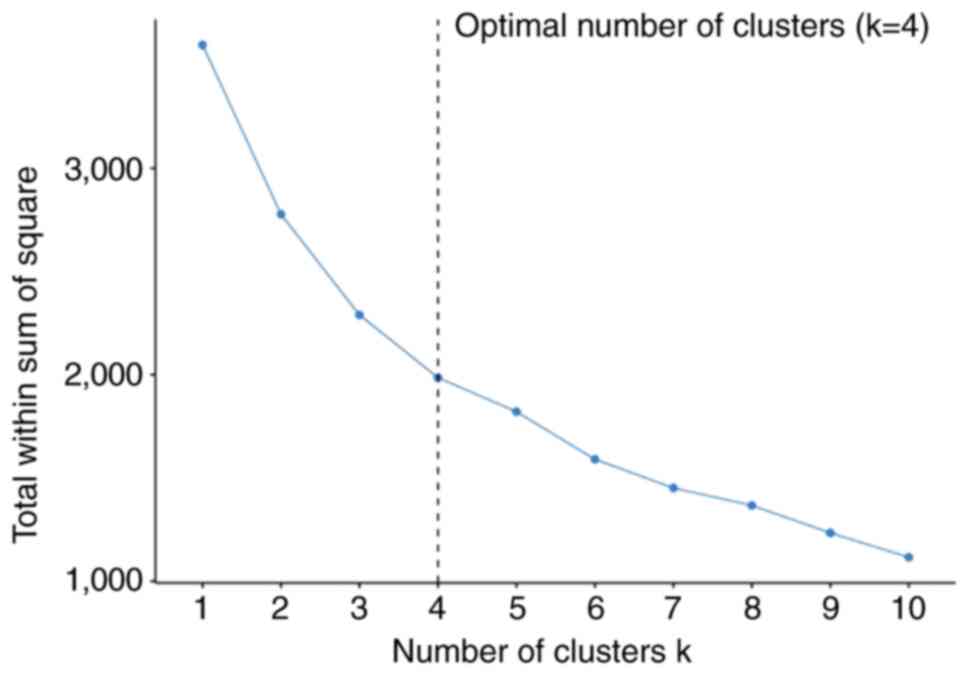
iv) Elbow method. There are many methods to determine the number of clusters, including the Elbow method, Silhouette coefficient, Gap statistic and fuzzy clustering. The Elbow method is an intuitive and simple approach commonly used to determine the number of clusters k of the K-means algorithm. The method classifies the data according to different k values by enumeration, after which the variance percentage of each classification is obtained and a chart may be drawn. The k value corresponding to the inflection point, the elbow, in the curve is selected as the best cluster number. Compared with the Elbow method, the Silhouette coefficient method considers both the similarity within clusters and the differences between clusters, whereas the Gap statistic method determines the appropriate number of clusters by calculating the Gap statistic for different numbers of clusters. The fuzzy clustering method is a membership-based clustering method that allows data points to belong to multiple clusters simultaneously. The k values provided by the Silhouette score and Gap statistic method were compared with the Elbow method used in the present study. Through comparison of the performance of these methods and considering the data, the Elbow method was ultimately chosen to determine the clustering parameters (Appendix S1; Fig. S1 and S2).

Process of model building

The distribution of radiotherapy set-up errors follows a normal distribution, which conform to the Gaussian distribution. Given the complexity of the data distribution, a single Gaussian model is evidently insufficient to represent the overall dataset, making the GMM a more suitable choice. As aforementioned, the K-means algorithm and GMM can be expressed in terms of each other under certain conditions, with K-means being a special case of GMM. GMM offers a stronger descriptive capability.

To construct the prediction model, the methodology outlined by Qiu et al (8) was adopted. After comprehensive evaluation and analysis of the various methods, the present study developed the error distribution prediction model through the following process: i) The IGRT set-up errors data of patients were recorded in three directions and converted into three-dimensional matrix data for saving and processing; ii) the number of clusters was determined using the Elbow method; iii) the K-means algorithm was used to cluster the raw set-up errors data, and both the cluster number and initial cluster center were obtained; and iv) the number of clusters and cluster centers obtained using the K-means algorithm were transferred as initial values to the GMM, while the EM algorithm was used for iteration to determine the parameters of the GMM and the clinical significance of the model was analyzed. The model building code is detailed in Appendix S2.

Calculation of the PTV expansion formula

PTV is an area expanded from the clinical target volume that accounts for positional deviations during treatment, respiratory motion and bladder filling changes (11,12). The ultimate goal is to ensure the tumor receives an adequate radiation dose. There are numerous methods available for calculating PTV, but the most commonly used one is the PTV margin formula recommended by Van Herk (13): M=2.5Σ + 0.7δ, where Σ is the standard deviation of the mean of the fractionation error for each patient, and δ is the root mean square of the standard deviation of the fractionation error for each patient. In the present study, the PTV margins were calculated based on the original error in each direction, and these were then compared with the GMM parameters. The aim was to verify whether the error range obtained through the constructed model could replace the PTV calculation formula, thereby simplifying the PTV calculation process. A flow chart of the research methods employed in the present study is shown in Fig. 1.

Figure 1. Flow chart of the research methods of the present study. GMM, Gaussian mixture model; PTV, planning target volume; LAT, lateral; LONG, longitudinal; VERT, vertical.

Data processing

In the present study, WPS Office Excel (version. 6.0.2; Kingsoft Office Software) was used for data collection and preliminary statistics, R language programming (version. 4.0.2; R Core Team) was used for K-means initial clustering and PyCharm (version 2020.1.2; JetBrains) was used for construction of the GMM and parameter solutions.

Results

Patient data

The clinical data of patients and the set-up errors data of IGRT for each fraction were obtained. All 80 patients were female and consisted of 36 patients with left-sided breast cancer and 44 patients with right-sided breast cancer. The age of the patients ranged from 26–67 years, with a median age of 47.5 years. A total of 1,200 sets of set-up errors data were collected for model construction.

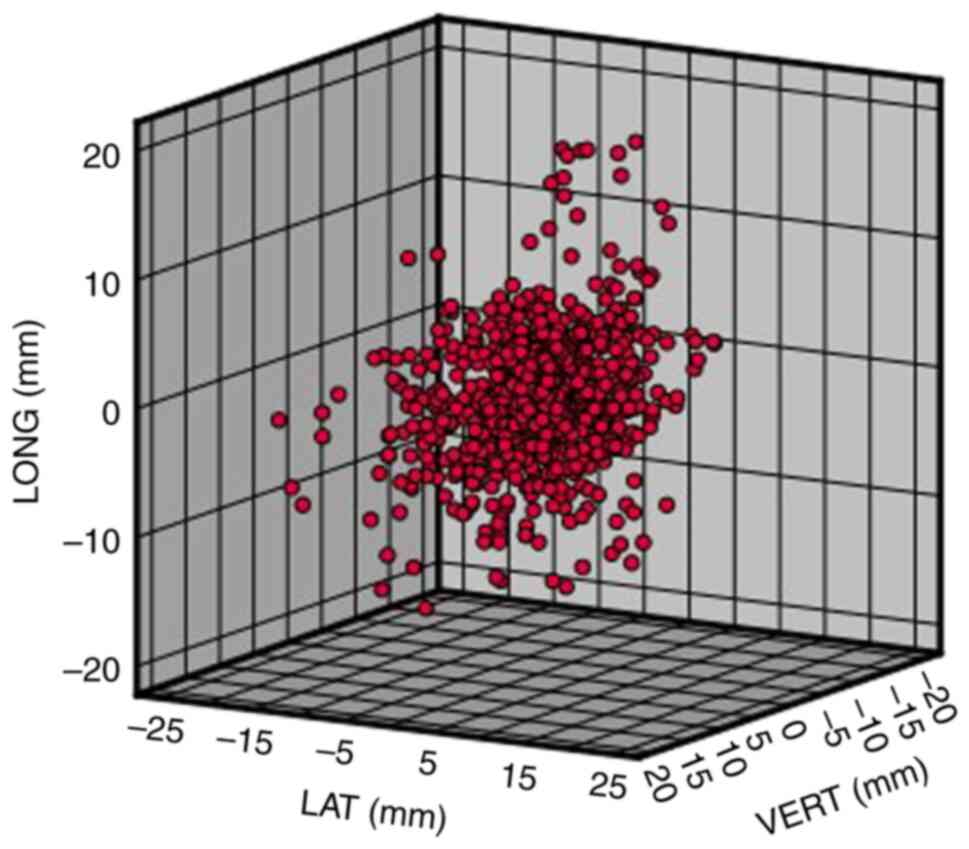
Raw error data matrix

The statistical results arising from the analysis of the 1,200 sets of set-up errors data that were collected from 80 patients with breast cancer are shown in Table I. Each patient's IGRT set-up errors data were recorded in the three directions of LAT, LONG and VERT, converted into a three-dimensional matrix and the distribution of the raw error data matrix obtained (Fig. 2).

Figure 2. Three-dimensional matrix distribution of raw set-up errors. The red dots represent the set-up errors data, which were converted into a three-dimensional matrix distribution map according to the LAT, LONG and VERT directions. LAT, lateral; LONG, longitudinal; VERT, vertical.

Table I. Raw set-up errors statistics (mm).

Table I.

Raw set-up errors statistics (mm).

Direction	Maximum, mm	Minimum, mm	P25, mm	P50, mm	P75, mm	X±S, mm
LAT	23.60	−22.70	−2.75	−0.90	1.78	−0.90±4.81
LONG	18.10	−17.30	−2.60	−0.70	1.30	−0.83±3.98
VERT	15.10	−17.30	−2.90	−1.30	0.80	−1.18±3.42

[i] LAT, LONG and VERT represent the directions for the raw set-up errors. LAT, lateral; LONG, longitudinal; VERT, vertical; P, percentile; X±S, mean ± SD.

Optimal clustering number

The K-means method was used to cluster the raw three-dimensional matrix errors data, and the optimal number of clusters determined using the Elbow method was 4. At this point (k=4), the internal variance decreased slowly, forming an inflection point and the clustering effect was good (data compactly clustered according to classification, with few discrete data) (Fig. 3). The data were clustered according to k=4 to obtain the initial cluster center and the clustering effect diagram (Table II and Fig. 4).

Figure 3. Selection of the optimal number of clusters according to the Elbow method. The results of application of the Elbow method to determine the optimal cluster number, k. As the cluster number increases, the within-cluster variance of sample partitions decreases gradually. When k=4, it reaches the position of the elbow on the curve, representing the optimal k value. At this point, the reduction in within-cluster variance slows down, and selecting this value helps balance clustering effectiveness and model complexity. k, optimal number of clusters.

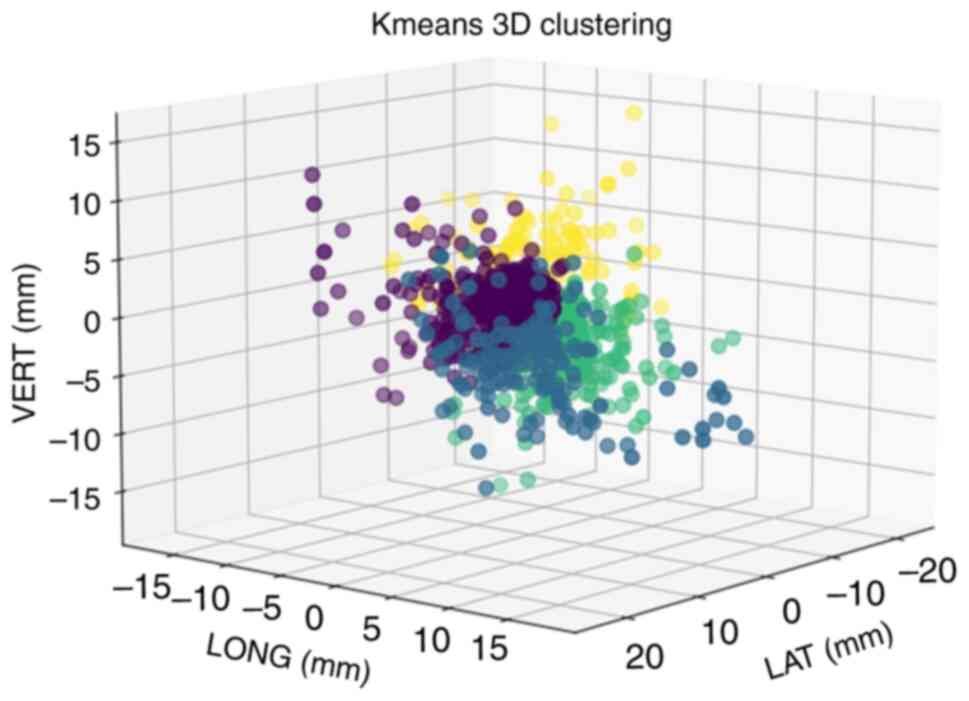Figure 4. Preliminary three-dimensional clustering results by K-means. LAT, LONG and VERT were used as axes to establish a three-dimensional clustering effect map, and the initial cluster center points were µ1, µ2, µ3 and µ4, which are represented by the purple, blue, green and yellow points, respectively. LAT, lateral; LONG, longitudinal; VERT, vertical.

Table II. K-means initial clustering center.

Table II.

K-means initial clustering center.

Center	LAT	LONG	VERT
µ1	1.20187967	−2.16093058	0.30402782
µ2	4.69122754	3.45807100	−3.39719418
µ3	−2.87421188	0.22517496	−2.87446722
µ4	−8.61301527	−5.27360414	2.21768811

[i] Data are clustered according to k=4 and the initial clustering center was obtained. LAT, LONG and VERT represent the directions for the raw set-up errors. LAT, lateral; LONG, longitudinal; VERT, vertical.

GMM for prediction of set-up errors distribution

The cluster number and cluster centers obtained using the K-means algorithm were passed to the GMM as initial values, and the EM algorithm was used for iteration to solve and determine the parameters of the GMM. The clustering effect and cluster center distribution are shown in Fig. 5. The parameters of the GMM error distribution prediction model obtained by solution are shown as follows: The center coordinates of each error, namely the mean µ of the GMM (Table III), the covariance matrix of the errors model, namely the GMM σ (Table IV), and each error center probability, the coefficient α of the GMM (Table V).

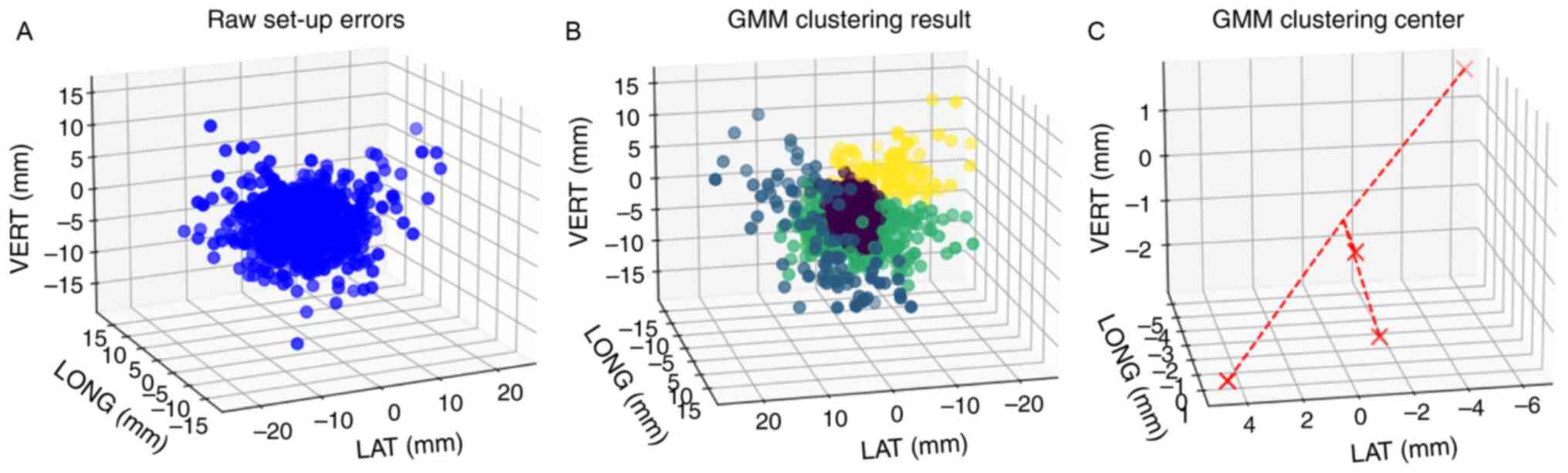Figure 5. Clustering results according to the GMM. (A) The clustering effect diagram of the raw set-up errors data is shown, where the blue dots represent the raw data. (B) The clustering effect diagram of the GMM. Data with initial clustering center points of µ1, µ2, µ3 and µ4 are represented by purple, blue, green and yellow points, respectively. (C) Distribution diagram of clustering center points of the GMM, with the 4 red crosses representing the clustering centers. GMM, Gaussian mixture model; LAT, lateral; LONG, longitudinal; VERT, vertical.

Table III. Center coordinates of set-up errors.

Table III.

Center coordinates of set-up errors.

Center	LAT	LONG	VERT
µ1	−0.55132442	−0.35566862	−0.7863227
µ2	4.59050708	1.47558872	−2.75250798
µ3	−1.56319372	−0.73935399	−2.73943799
µ4	−6.30437674	−5.40364623	1.72933048

[i] LAT, LONG and VERT represent directions for the raw set-up errors. LAT, lateral; LONG, longitudinal; VERT, vertical.

Table IV. Covariance matrix of the Gaussian mixture model.

Table IV.

Covariance matrix of the Gaussian mixture model.

Center	LAT	LONG	VERT
σ1	4.05961107	0.55761847	1.04514747
	0.55761847	3.99255928	−0.81082324
	1.045147478	−0.81082324	3.58734632
σ2	29.05573717	−6.72025397	14.63273482
	−6.72025397	48.16645234	−12.44937602
	14.63273482	−12.44937602	28.24677334
σ3	31.2592853	−2.90156674	0.63680924
	−2.90156674	12.48825079	−2.49353153
	0.63680924	−2.49353153	10.83415154
σ4	28.71612318	−1.77487288	−9.93513094
	−1.77487288	18.70292861	3.01798682
	−9.93513094	3.01798682	18.34102576

[i] LAT, LONG and VERT represent the directions for the raw set-up errors. LAT, lateral; LONG, longitudinal; VERT, vertical.

Table V. Each error center probability.

Table V.

Each error center probability.

Center	σ1	σ2	σ3	σ4
Probability	0.53169465	0.11099651	0.24059103	0.11671781

Prediction of PTV expansion

The reference PTV margins based on the raw set-up errors in each direction were calculated and compared with the GMM parameters, where Σ is the standard deviation of the mean of the fractionation error for each patient, and δ is the root mean square of the standard deviation of the fractionation error for each patient (Table VI).

Table VI. Reference value of the PTV margin (mm).

Table VI.

Reference value of the PTV margin (mm).

Direction	Guidance frequency, n (%)	Σ	δ	MPTV, mm
LAT	487 (40.58)	1.71	2.33	5.90
-LAT	713 (59.42)	2.05	2.89	7.16
LONG	493 (41.08)	1.83	1.56	5.67
-LONG	707 (58.92)	1.65	2.43	5.82
VERT	399 (33.25)	1.24	1.61	4.23
-VERT	801 (66.75)	1.76	2.08	5.87

[i] LAT, LONG and VERT represent the directions for the raw set-up errors. PTV, planned target volume; LAT, lateral; LONG, longitudinal; VERT, vertical; -, negative; Σ, the standard deviation; δ, the root mean square; M_PTV, reference value of the PTV margin.

Discussion

The present study utilized the GMM to establish a predictive model for the distribution of set-up errors in IGRT for breast cancer. The analysis of the data obtained confirmed the feasibility of the GMM use for quantitative description and predictive analysis of set-up error distribution in breast-cancer IGRT. By comparing these results with the conventional PTV margin calculation formula, the present study demonstrated the clinical application value of GMM. This offers a reference for controlling set-up errors and determining PTV margins in breast cancer radiotherapy, especially in cases without routine daily image guidance.

Concerning the GMM parameters, it was found that the set-up errors were mainly in the direction of four central points (µ1-µ4). The spatial coordinates of each center could reflect the average offset direction and offset of the points in the center. For example, the deviation of µ1 in each of the three directions (LAT, LONG and VERT) was within 1 mm, recorded as −0.55, −0.36 and −0.79 mm, respectively. From the overall center distribution data, all the raw errors in the LAT, LONG and VERT directions were −6.3-4.60, −5.40-1.47 and −2.7-1.7 mm, respectively. According to the probability of each center, the most possibility of the set-up errors in the µ1 direction was 0.53, and for the other three centers (µ2, µ3 and µ4), the highest possibilities were 0.11, 0.34 and 0.12, respectively. The covariance matrix reflects the magnitude of the standard deviation. According to the covariance parameters of the GMM, the maximum statistical standard deviation of the set-up error could reach 29.06. Compared with previous studies, Qiu et al (8) constructed a predictive model for set-up error distribution in pelvic tumor radiotherapy using the GMM on the Varian Novalis Tx® linear accelerator. The center point coordinates in the three directions were −1.85-0.72, −2.41-1.54 and −3.88-4.28 mm, respectively. In the present study, the errors were relatively larger, which may have been associated with greater mobility of the breast tumors. Compared with pelvic tumors, breast tumors exhibit greater movement, highlighting the necessity for image guidance and set-up error prediction in breast cancer radiotherapy.

Traditional image-guided methods involve acquiring real-time images and registering them with reference images from the treatment plan. CBCT and MRI registration provide high-precision 3D image guidance but come with high equipment costs, additional radiation and long imaging times (5). Deep learning-based methods, using Convolutional Neural Networks for image segmentation and registration, offer high accuracy and automation, but require large, labeled datasets and significant computational resources (14). In contrast with traditional image-guided methods for assessing set-up errors, the present study investigated radiation risk using a constructed predictive model (4). The GMM serves as the foundation, utilizing the Gaussian probability density function (also known as the normal distribution curve) to decompose observed phenomena into multiple components, accurately describing their characteristics (15). Theoretically, regardless of the distribution pattern within the observed dataset, the GMM can fit it through combining multiple Single Gaussian Models linearly. In contrast to other predictive models such as deep learning, the GMM offers simplicity, speed and the ability for quantitative analysis (16,17). Various techniques exist for determining the optimal number of clusters, including the Elbow method, and the Silhouette coefficient, the Gap statistic and fuzzy clustering methods (18). The Elbow method involves classifying data with different values of k, calculating the variance percentage for each classification and plotting a graph. The optimal number of clusters corresponds to the ‘elbow point’ on the curve, providing an intuitive and comprehensive solution (19). Consequently, the Elbow method was selected for the present study to determine the appropriate number of clusters. Notably, set-up errors during radiotherapy significantly impact treatment accuracy (4). The set-up error during radiotherapy is a critical factor affecting treatment accuracy. Small et al (20) proposed a method for analyzing the distribution of radiotherapy errors and pointed out that different sources of errors lead to different characteristics of the distribution of errors. Van Herk (13) focused on the effects of systematic and random errors in radiotherapy and investigated a variety of mathematical models to describe the errors. The systematic error is the mean of all fractional set-up errors, whereas the random error is the standard deviation of these errors, reflecting the diversity and variability of these errors. However, set-up errors do not manifest as simple three axial deviations. In the present study, statistical and modeling methods were used to deeply study the distribution of IGRT data. It was found that the set-up errors not only exist in the three axes, but also tend to be concentrated along the specific center direction, and the deviation distribution probability of each center direction is different. This finding suggested that the set-up errors had a more complex distribution form, which is no longer limited to the triaxial linear deviation, but may involve more dimensional and directional changes. This deeper understanding of the error provides a more specific and targeted plan for further error correction and treatment optimization.

For validation of the prediction model and to assess its clinical applicability, the effectiveness of the model was assessed by comparing it with a commonly used clinical formula for calculating the PTV expansion margin. The results indicated that the PTV expansion margins determined using Van Herk's formula in six directions were as follows: LAT, −7.60 and 5.90 mm; LONG, −5.82 and 5.67 mm; and VERT, −5.87 and 4.23 mm. These findings aligned with the results derived from the GMM analysis, with deviations ranging from 0.42-4.20 mm. The largest deviation occurred in the VERT direction. Although the error in this direction was larger, the distribution was more concentrated, leading to discrepancies between the model predictions and the formula calculations. Numerous factors are known to affect set-up errors during radiotherapy. For breast cancer, in particular, the unique shape and position of the breast, along with its large range of motion, result in set-up errors that are significantly different from those of other thoracic tissues (21). A study performed by Chen et al (22) on 113 patients with breast cancer undergoing radiotherapy investigated the influencing factors and uncertainties of set-up errors. This analysis demonstrated that body mass index, the surgical method, surgical site and immobilization method may affect the accuracy of radiotherapy for breast cancer. As a key image-guided device, CBCT can monitor and correct set-up errors in real time (23). Although CBCT has a high utilization rate and low radiation dose, it still utilizes ionizing radiation, which may increase human radiation exposure, thereby increasing further the risk of second primary tumors. Donovan et al (24) reported that the doses to the breasts, heart and lungs of patients with breast cancer during CBCT scanning were approximately 1.7-23.2, 4.0-21.6 and 0.8-22.8 mGy, respectively. Multiple exposures increase the radiation dose significantly, which may lead to the development of second primary tumors (24). In order to resolve this problem, a statistical modeling analysis of the raw error data of patients who underwent complete IGRT treatment was performed in the present study to present the error distribution law and predict the error probability. The present study validated the applicative value of error prediction ranges through calculating the PTV expansion margins. This served to optimize the PTV boundaries, thereby preventing issues of excessive or insufficient PTV expansion that could lead to dosage deviations in the target area in clinical settings (25,26). In addition, the present study suggested that the PTV expansion should not only be limited to the three axial errors, but that the directions and variances of the four offset centers should also be comprehensively considered for PTV expansion. Specifically, a non-uniform expansion strategy is required to cover the variance offset in each center direction. The goal of this approach is to comprehensively consider the potential sources of error during radiotherapy, thereby providing a more complete understanding of the requirement for PTV margins. Through the integration of the error changes in multiple directions, not only can the effect of the error be better controlled in planning, but it also helps to optimize the treatment plan, thereby ensuring adequate target coverage while minimizing the damage to the surrounding normal tissues.

Although the present study attempted to use the GMM to predict the distribution of errors in radiotherapy, optimize PTV expansion margins and improve radiotherapy accuracy, certain limitations still need to be addressed. First, regarding sample size, 80 patients were included and 1,200 data sets collected, which, although relatively large, still presents certain limitations in terms of model construction and data prediction. Future work will involve collecting more samples and conducting in-depth analyses of the data to uncover potential differences among subsets, with the goal of enhancing the model's robustness and accuracy. Secondly, both the K-means algorithm and the GMM were initialized in a random manner, so the initial state may have been random, leading to different final results. Although ‘random_state=0’ was set for both methods in the present study to ensure the reproducibility of the results, this only applied to multiple runs on the same computer. Differences on different computers, such as the implementation of the underlying libraries, operating systems and processor architectures, can lead to different behaviors. In addition, the library version is an important consideration, as it must be made certain that the libraries, such as sklearn and pandas, are installed as the same version on all computers. Different versions of libraries may have different default parameters, optimizations or fixes, and these differences may affect the stability of the results. Therefore, when replicating the present study, there may be differences in the results using different versions. In the future, we will also test the data on different versions and analyze the differences.

In conclusion, the present study emphasized the importance of accurate error control in radiotherapy, and discussed IGRT technology and its limitations in depth. GMM can be used to quantitatively describe and predict the distribution of set-up errors in IGRT for breast cancer, thereby providing a reference for the set-up errors control and tumor planning target expansion of breast cancer without routine daily image-guided radiotherapy. The results of the present study are beneficial to reduce the extra radiation of breast cancer radiotherapy and improve the treatment accuracy, and can be applied to other tumors. Future studies could introduce deep learning methods to more accurately predict and control radiotherapy errors. Techniques such as anomaly detection and pattern recognition may be employed for a more in-depth analysis of images and error data (27,28). Currently, studies are developing in the direction of multi-factor analysis, comprehensively considering the angle error and physiological changes, and performing more detailed data analyses to understand the sources of errors and to change the rules more comprehensively.

Supplementary Material

Supporting Data

Acknowledgements

Not applicable.

Funding

The present study was funded by Fujian Province Health Youth Research Project (grant no. 2022QNA018) and Fujian Medical University Sailing Fund General Project (grant no. 2022QH1029).

Availability of data and materials

The data generated in the present study may be requested from the corresponding author.

Authors' contributions

FD and JC drafted the manuscript and worked on the conception, design and interpretation of data. FD and JC confirm the authenticity of all the raw data. ZY and FL helped with data processing and drafting the manuscript. XL and YW reviewed the data analysis. All authors contributed to the article. All authors read and approved the final version of the manuscript.

Ethics approval and consent to participate

The present study was retrospective and was approved by the Ethics Committee of Fujian Medical University Union Hospital (Fuzhou, China; approval no. 2022WSJK017). The data used in the study did not interfere with the patient's treatment and the Ethics Committee waived the requirement for informed consent. All procedures involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Declaration of Helsinki and its later amendments or comparable ethical standards.

Patient consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

References