Introduction: Hyperthermia therapy in
oncology
Hyperthermia is an ancient method; in fact, it was
the very first medical treatment in human medicine. Despite its
long history, this approach currently has no widespread
applications and is on the periphery of the medical therapies. This
contradiction characterizes the history of hyperthermia in
medicine.
The use of hyperthermia as a therapy has various
stumbling blocks as the effect caused by the absorbed heat is too
complex; the applied, absorbed energy is usually depleted
non-homogeneously, and the intricacy of biological processes
modifies the intended impact of application. The heating process
itself represents a further complication: The efficacy indeed
differs by the heat source and by the properties of the target
volume and its physiological effects. Hyperthermia treatment
modalities have yet to progress from a bio-medical experiment to a
clinically proven treatment (1,2).
The effect of hyperthermia is not straightforward in
in vivo experiments and is even more complex in clinical
practice. In clinical applications, hyperthermia has two essential
effects: i) Thermal damage assessed by the Arrhenius approach and
associated evaluations; and ii) physiology-dependent effects are
improving the complementary applications.
While the simple thermal effect can be demonstrated
using in vitro experiments, the evident clinical outcomes
are not clearly observable. The challenge is the negative
physiological feedback of systemic reactions, which tries to
compensate for the increase in temperature and reassert thermal
homeostasis.
Hyperthermia is a technically challenging treatment
modality. Energy absorption during the heating process entirely
depends on the technique applied, and there is no unified protocol
for the various technologically determined targets of the heat. The
ablation technique differs from the methods causing necrosis or
apoptosis, or those that heat up the whole body into the fever
range. The category 'hyperthermia' includes the group of
energy-absorption methods, and the individual solutions of
absorption require an actual protocol. It is very similar in this
regard to the chemo-variants of oncological therapies.
Chemotherapy, depending on the targets of the drug, has different
protocols. Mixing these can cause severe adverse effects and even
fatal events, such as poisoning. Homogeneous targeting in most of
these therapies requires very different protocols than local or
cell-sensitive selection. For example, chemotherapy is administered
intravenously at different doses than with chemoembolization or
other types of local administration. Isodose homogeneity, as in
radiotherapy, is also not used in most of the brachytherapies,
radiation seed or nanoparticle administration. We are sure that the
hyperthermia variants also have specific differences in their dose
and protocol, sharply depending on their technical solution and
targeting method. Defining a general dose and protocol for all
hyperthermia methods is a misleading request. The methods are not
equal, their effects are different, and thus the dose and protocol
have to fit the specific situation.
Oncological hyperthermia suffers presently multiple
problems (3), among these the lack
of underlying mechanisms of thermal therapies and the missing joint
definition of the method and missing a well measurable dose for
clinical and research applications.
The choice between thermal or non-thermal
and between heat or temperature
The definition of oncological hyperthermia is not
unified in the actual literature. The following are a few of the
most common definitions found in the literature: i) Hyperthermia is
the use of therapeutic heat to treat various types of cancer on and
inside the body (4); ii)
hyperthermia is the overheating of the body (5); iii) hyperthermia (also known as
thermal therapy or thermotherapy) is a type of cancer treatment in
which body tissue is exposed to high temperatures [up to 113°F
(45°C)] (6); iv) hyperthermia
therapy is a type of medical treatment in which body tissue is
exposed to slightly higher temperatures to damage and kill cancer
cells or to render cancer cells more sensitive to the effects of
radiation and certain anti-cancer drugs (7); v) hyperthermia involves body
temperature which is much higher than normal and is either induced
therapeutically or iatrogenically (8); vi) hyperthermia occurs when cells in
the body are exposed to temperatures which are higher than normal,
and thus changes take place inside the cells (9).
The indefinite definition ranges in a broad spectrum
of targets, heating the body, cancer or the malignant cells, and
mixes the therapeutic heat and the therapeutic temperature. The key
to thermotherapy is the amount and distribution of the absorbed
energy in the malignant target. We prefer the definition of
oncological hyperthermia as method with which to kill malignant
cells by heat-inducing absorbed energy and/or sensitize specific
complementary therapies.
The majority of the oncological hyperthermia methods
work with absorbed energy by bio-electromagnetic interactions. The
biological processes are fundamentally based on the only
electromagnetic working ability. Bio-electromagnetic energy
exchange is a broad category of energies in life, including all the
chemical, mechanical, thermal and bio-electric changes energizing
the living processes. The absorption of external energy is
necessary for life, it forms an open system; it does not exist in
an energetically closed (self-sustaining) mode.
Energy is a global category for all possible work
processes. Heat is a type of energy, which can raise the
temperature of the target, although not always. An increase in
temperature is not the only effect in this complex interaction. The
absorbed energy may be utilized for structural rearrangement or
chemical reactions, or electromagnetic changes (such as
polarization). The temperature strongly depends on how the heat is
provided to the system, and how well the system is isolated from
its environment. Heat can be transformed into complex changes in
the target without an increase in temperature.
A simple example is boiling water. The water reaches
its boiling point of 100°C, and its temperature from that time
continually remains at 100°C; all the heat pumped in is used for
evaporation (steam production). The energy is ultimately used to
change the structure of the material from solid to liquid.
Temperature is not the heat or even energy of the
system. It measures the average energy of the particles in a
system. The average does not mean that every particle has the same
energy in the equilibrium. The statistical average works
differently. For example, the average yearly income in a country
does not mean that everyone's salary is the same, and the average
does not measure your level of earnings.
Absorbed energy differs from temperature, i.e., the
average kinetic energy of particles. A good example is a comparison
of warm water in a swimming pool and the same temperature of water
in a glass. Heating up the pool needs much more energy than heating
up a glass of water to the same temperature. Although heat and
temperature are different, these are used equivalently in many
instances. The main reason for confusing them is fixed attention to
simple situations when the heat does not perform any ‘work’ in the
system's internal energy; it is only homogeneously converted to the
average, to the temperature. The energy averaging and
characterizing the process by the temperature can happen when we
heat clean water between its freezing and boiling points. However,
this simple case is very far from the complexity of the living
material, which is heterogeneous and uses absorbed heat energy for
structural and chemical changes.
Using the temperature like a dose of heating is
incorrect; dosing by temperature does not depend on the volume or
mass of the target as it is an average and is the same in half or
any fraction of the target, while the dose must be different for
different sized targets. Due to this, heat is a good candidate for
dosing.
Keeping in mind the example of boiling water,
holding the temperature at 100°C while pumping in a massive amount
of energy to keep the water boiling is a thermal process, although
the temperature does not change. The question thus automatically
arises as to what is the proper characteristic that we define as
‘thermal’ when the temperature is not a stable indicator of
a thermal process. The molecular mechanism of the thermal process
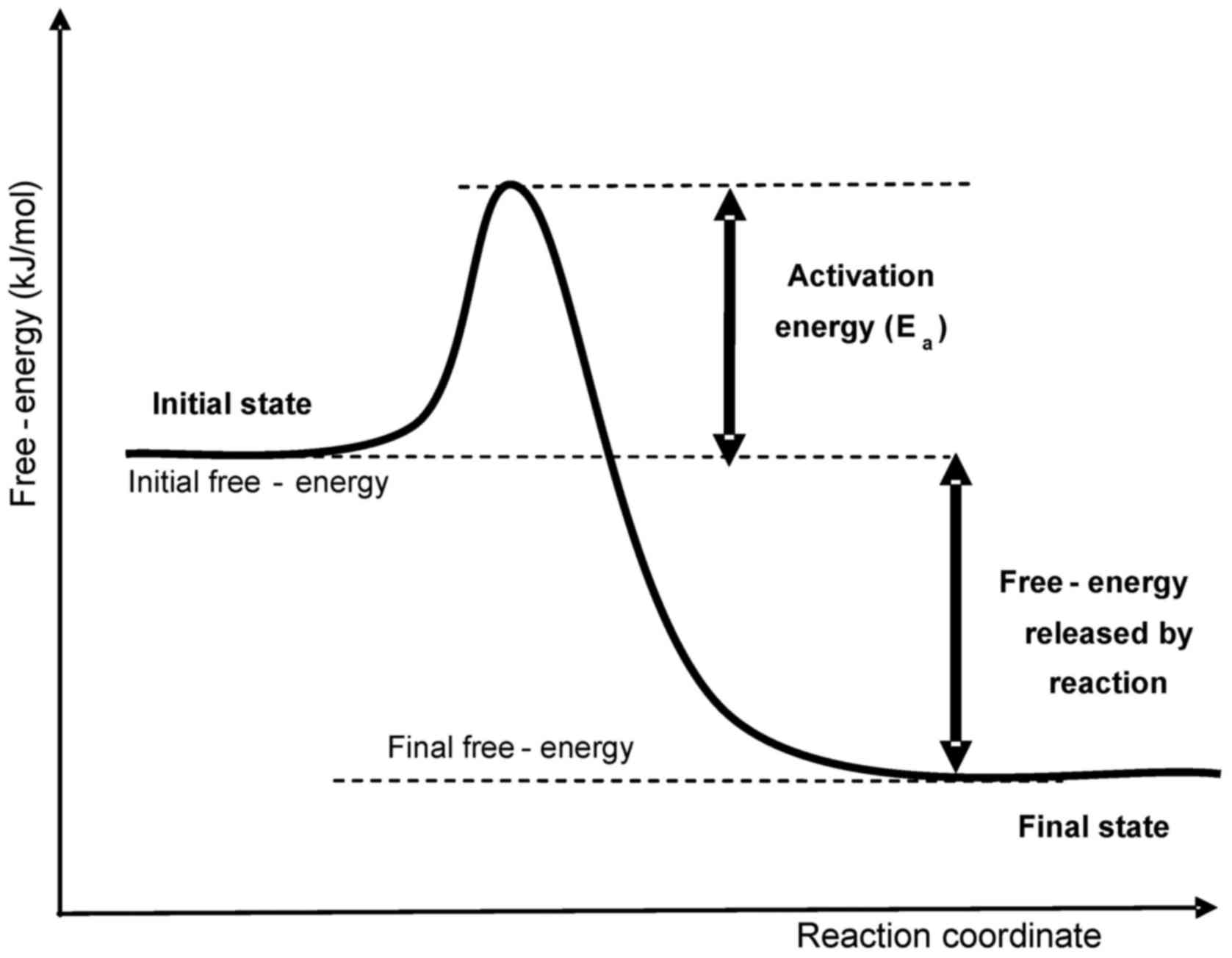
defines the probability (reaction rate, kr) of a
jump of a given particle through an energy barrier (activation
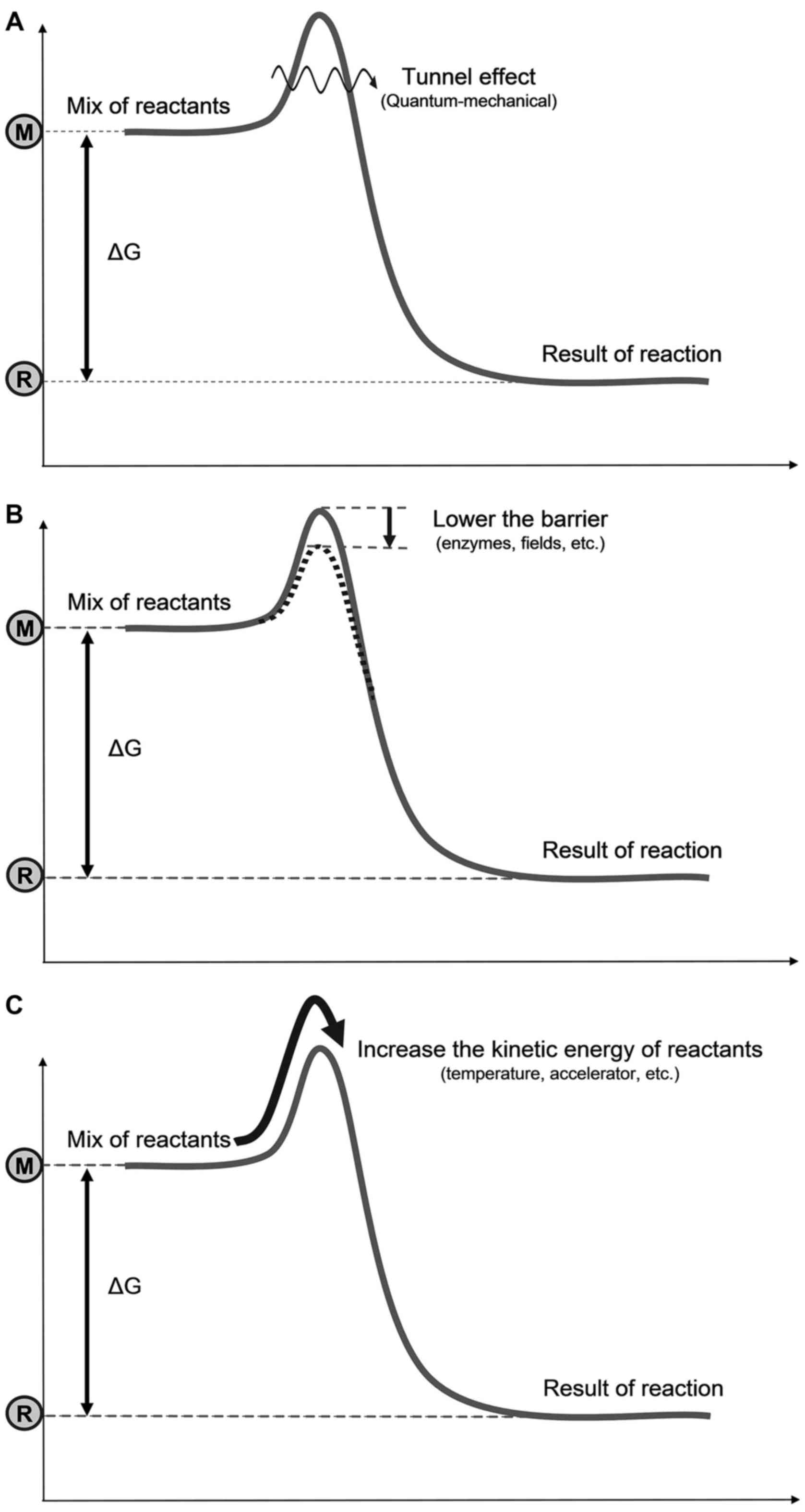
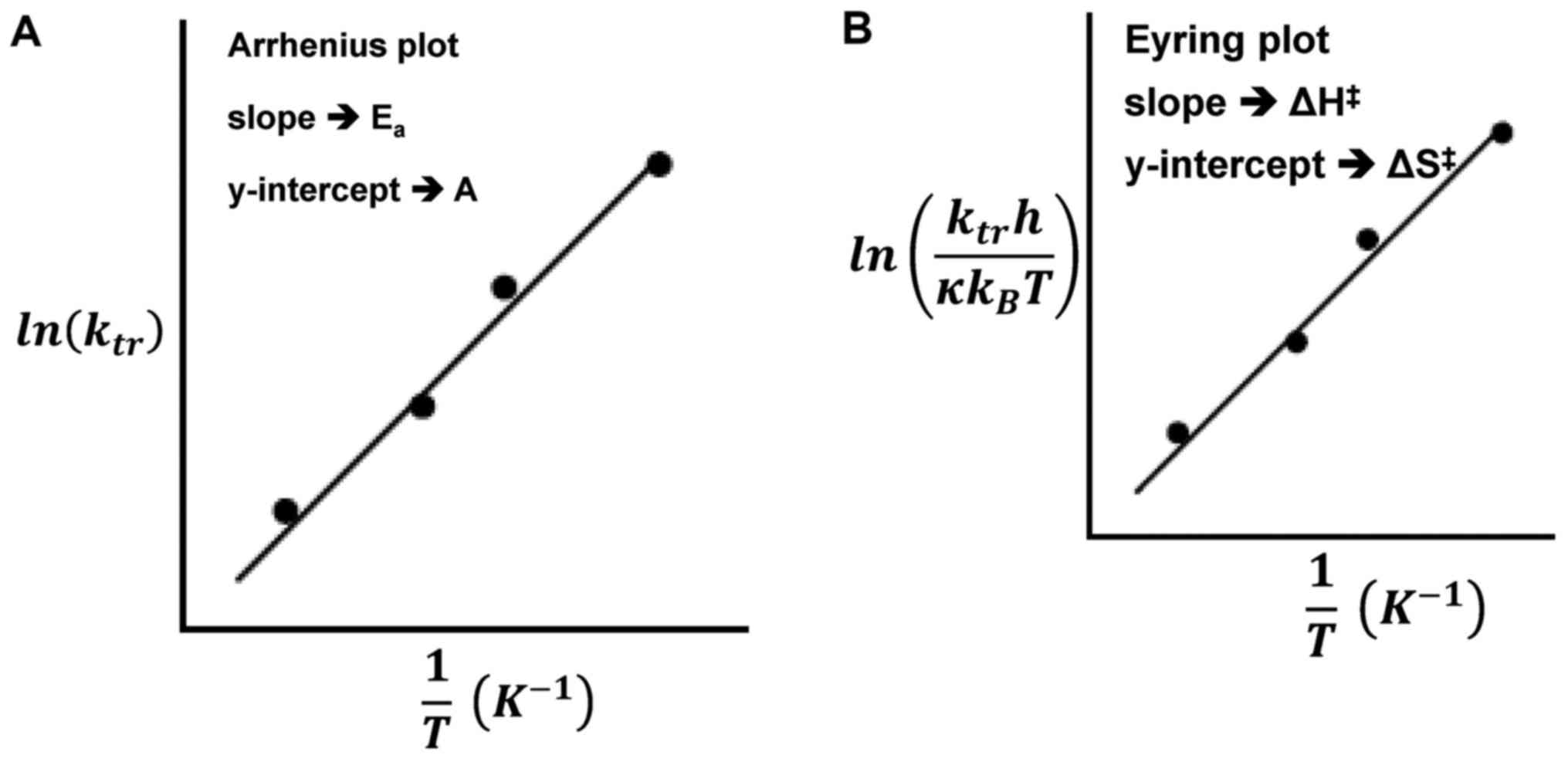
energy, Ea, measured in J/mol) (Fig. 1).
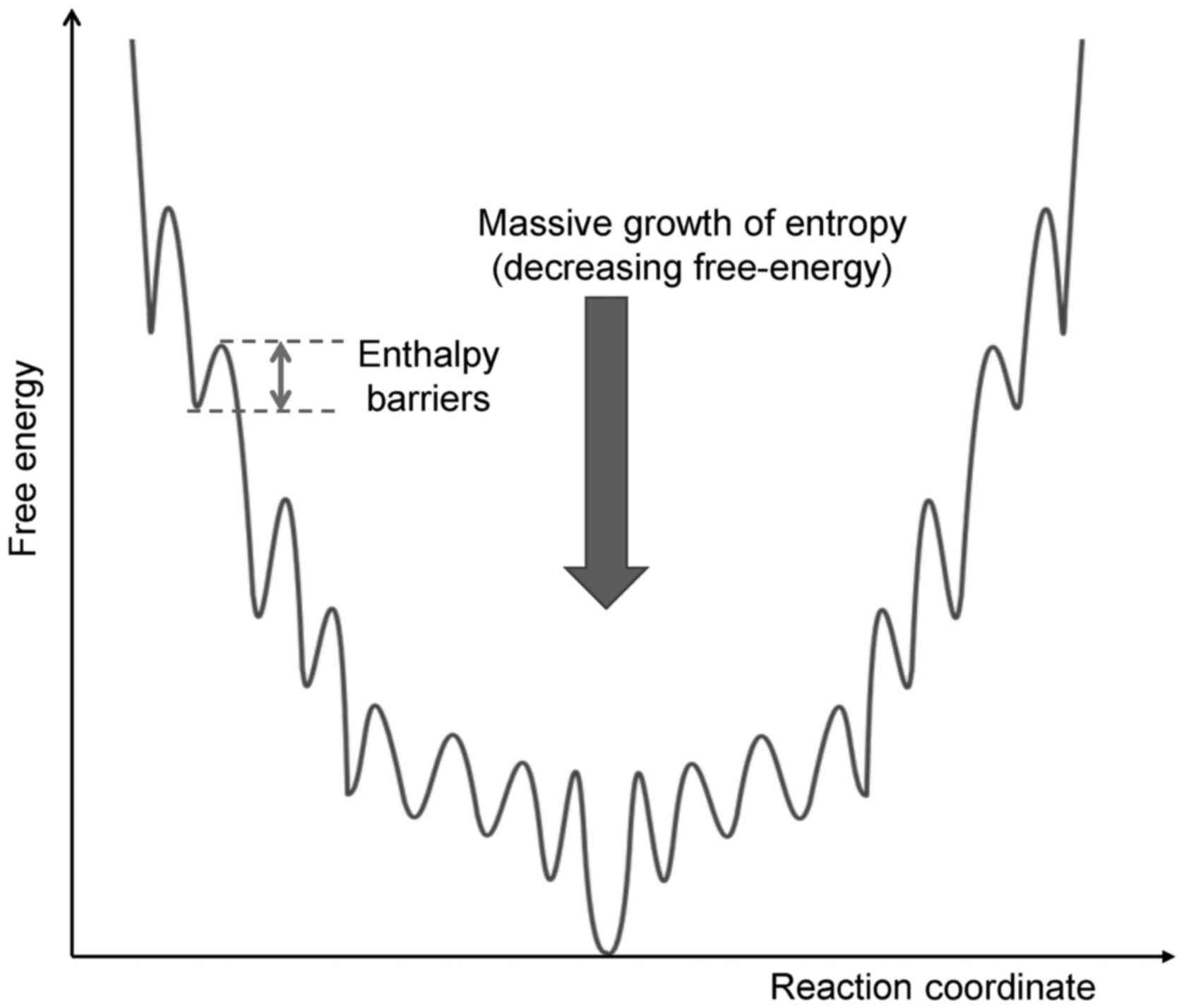
The energy barrier is mandatory for life processes;
without it, an immediate reaction occurs, which explosively drives
the reaction out of control. A living system has a funnel-type
multibarrier system that gradually loses energy step-by-step during
a jump through various reactions in a chain (Fig. 2).
Thermal processes are described by an empirical
description of the reaction rate, i.e., the Arrhenius equation
(10); [Equation 1]:
kr=Ae−EαRgT
where T is the absolute temperature, (measured in K),
Rg is the universal gas constant
(Rg=8.314Jmol⋅K)
and A is the ‘pre-exponential factor’ which defines the
frequency of collisions, describes the irreversible jump, and
measures its dimension in [1/sec]. The Arrhenius equation is an
empirical observation, but is precise for most practical
applications (
11). A detailed
history and trends have been described (
12).
Three possible mechanisms are available to go over
the barrier (Fig. 3): i) Bypass
the barrier: A quantum-mechanical (tunneling effect),
non-temperature dependent solution (13); destroy or lower the barrier, or
form an intermediate compound (transition state); Provide ease for
going over the barrier; promoted chemically (e.g., enzymes),
electromagnetically (e.g., an electric field), or by other effects;
this is a non-temperature dependent solution; iii) surmount the
barrier: i.e., A temperature dependent solution by increasing the
kinetic energy of the reacting particles, by accelerating them
individually or increasing their average kinetic energy
(temperature). Note that two of these three mechanisms are not
temperature-dependent, but are clearly energy consuming; thus, they
are thermal.
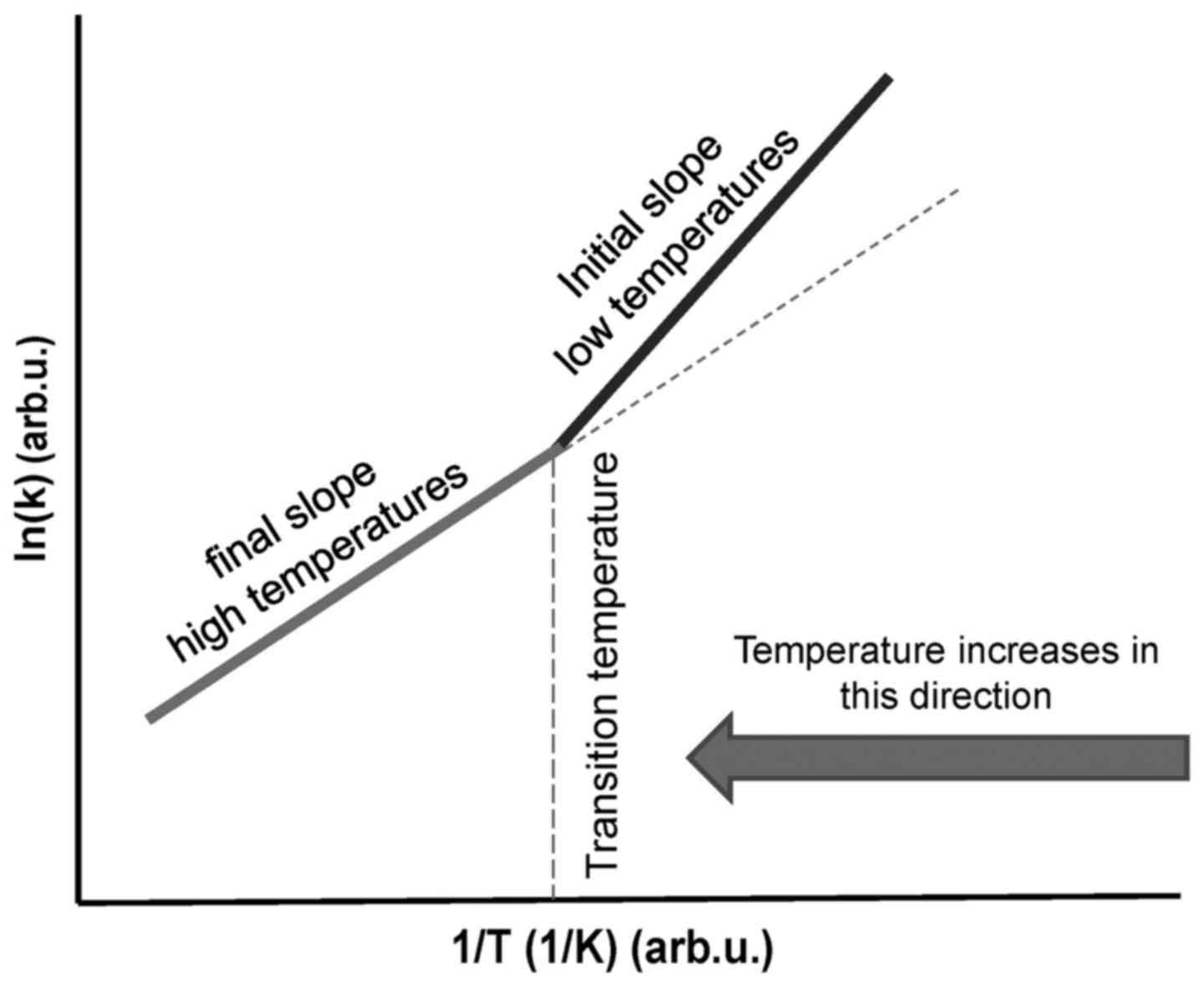
When a phase transition occurs, the activation
energy (Ea) changes and a kink appears on the
straight line (Fig. 4). The
temperature of the kink is responsible for the transition, and the
system remains at this point until the complete transformation has
been performed. The kink in the Arrhenius plot is not fixed at a
particular temperature, as it may be shifted by various heating
processes and by chemotherapy (14) or other chemical conditions
(15) that modify the actual
reaction (16). An electric field
also may affect the kink of the Arrhenius plot (17). The Arrhenius kink, which must be
overheated, corresponds well to the believed cellular phase
transition observed at around 42.5°C (18).
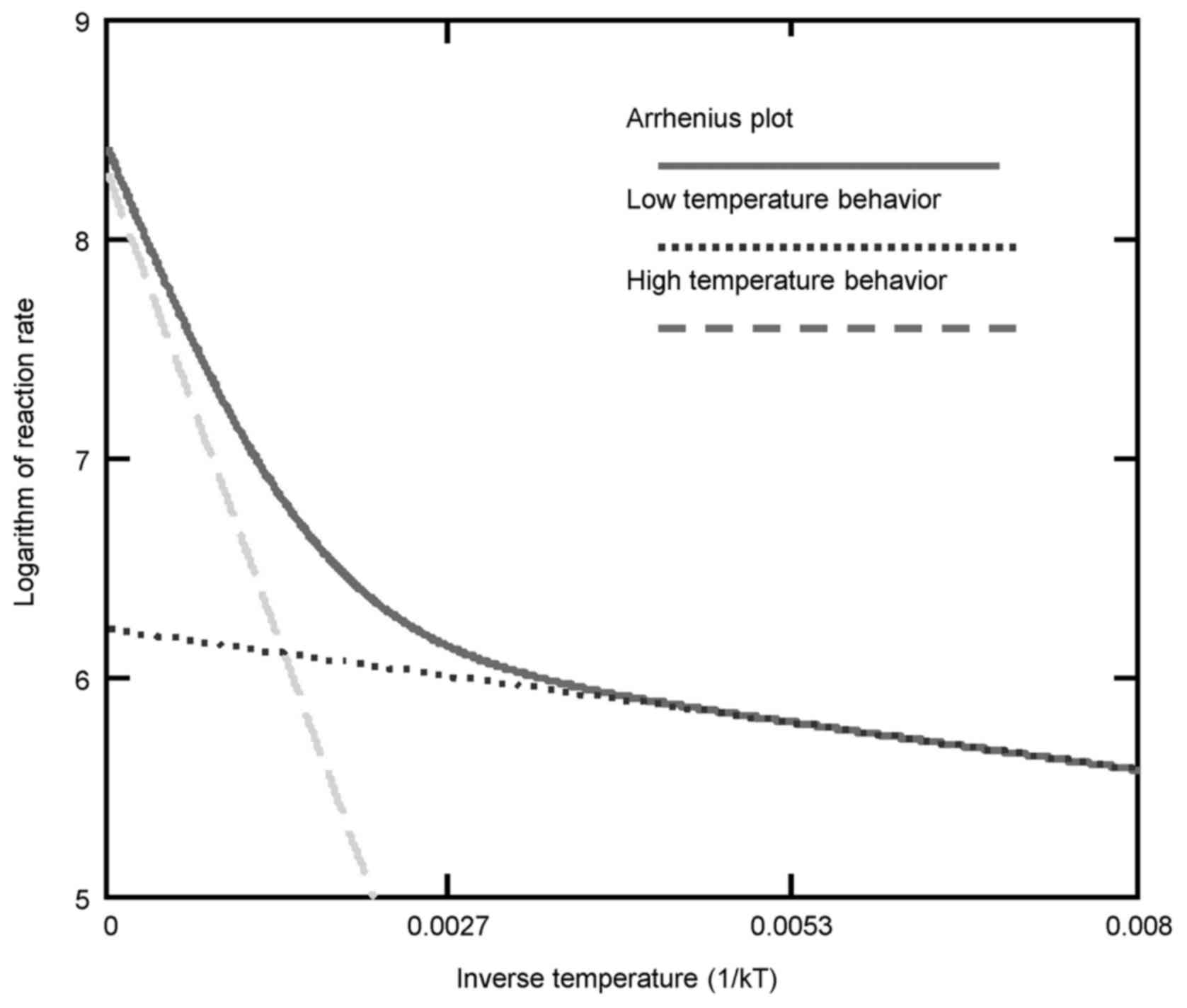
When the transition occurs non-homogeneously in the
system, then the kink is not a point; it will appear as a curvature
on the plot (19,20). The coexistence of two phases could
occur for a wide range of temperatures, and then two (or more)
Arrhenius lines combine to form the curve (Fig. 5).
When the reaction coordinates change, the system can
be approached by the empirical Arrhenius functions. In this case,
the process is definitely thermal. Sometimes categories of
‘non-thermal’ or ‘athermal’ effects are incorrectly
used when the process is thermal but non-temperature-dependent.
The internal energy (U) of a system has a
substantial variety of physical effects to be changed [Equation
2]:
where Yi and Xi are
thermodynamic variables, intensive and extensive characters of the
i-th component of the system, respectively. Possible
intensive values could be pressure (p), temperature
(T), chemical potential (μ), the electric field
(E) or the magnetic field (H), while
the extensive values (in order of their pairing with adequate
intensives) are the volume (V), the entropy (S), the
particle number (N), the polarization (P) and
the magnetization (M). These thermodynamic values add
energy terms to the internal energy in individual pairs, and thus
the internal energy with some of the interactions is as follows
[Equation 3]:
ΔU=pΔV−TΔS+μΔN+EΔP+HΔM
This type of non-temperature dependent case occurs
in transitions when the internal energy changes at a constant
temperature.
Determining the correct the dose of
hyperthermia
A well-defined and strictly scientific dose of
hyperthermia therapy is a critical issue in research and is crucial
to the future of hyperthermia in oncology (21). The proposed general definition of
oncologic hyperthermia is forcing cell-damaging energy absorption
on malignant cells and sensitizing other therapies. Accordingly, we
have to control the damaging thermal effect on malignancy by an
appropriate dosing process.
Consequently, the proper dose must be readily
applicable to all technical solutions and reliably measured under
standard hospital conditions. It must be measured quickly, with
acceptable accuracy, and it has to be the basis of the comparison
of different treatments by technical variants in clinical
prac-tice. The proposed dose at present (22-24)
is the cumulative equivalent minutes referring to 43°C:
CEM43Tx (measured in minutes). It contains two parts. The
CEM43 part is a time-dependent function FCEM43°C(V,t)
[Equation 4]:
where V is the volume of the target (the energy is focused
on the tumor mass; we assume that only the tumor volume is heated),
t is the time and T(τ) is the time-dependent
temperature, measured in °C. The R-value is fixed from the kink of
the Arrhenius curve measured by in vitro experiments on
Chinese hamster ovary cells (
25).
The FCEM43°C(V,t) function of Eq.4
is extended by a space-time dependent function
Tx(V,t), where is the V is the volume of
the tumor and x is given in % indicating the average
percentage of monitored sensors (Vx portion of
the tumor volume) in the V-volume where the temperature is
on average Tx(V,t) [Equation 5]:
where Vx is the volume, where the temperature of
the monitored sensors on average is Tx(V,t) and
thus x=100Vx/V [%].Tx(V,t) is
approximated mainly by guessing, and is usually guessed
independently of time characterizing the percentage of the tumor
which obtains the given minutes by CEM43°C. The missing
parameter is real-time mapping, which could change the
Tx(V,t) function in real-time, and would be
necessary for a correct determination. Due to inhomogenous heat
distribution, Tx decreases by growing monitored
volume V. The dose is finally [Equation 6]:
CEM43Tx=FCEM43°C(t)[min],condition:Tx(V,t){[°C],[%]}
which is measured in minutes, but additionally considers the
Tx(V,t) conditional function as a reference of
in vitro necrosis at 43°C and two other physical units: A
unit for the temperature (K or °C) and a unit for the
portion of the isothermal average x (%). For example,
CEM43T90 measures the cumulative equivalent minutes
referring to necrotic cell killing at 43°C when the measured
temperature is actually T90 in 90% of the
monitored sites (referred to as the thermal isoeffect dose in 90%
of the area) (
23).
This does use the time in non-conventional units
(min instead of sec), and the unit is rigorously somehow a mixture
of time and percentage. Non-linear physiological feedbacks need
real-time measurements, which are also requested due to the
integrative basis of the CEM43Tx dose.
Furthermore, this dose value requires registering the temperature
distribution of the target in space and time, which is practically
not measurable.
Taken together, given the abovementioned challenges,
the CEM43Tx dose has another severe scientific
problem: The T(τ) has of course a dimension, °C. When
we measure the temperature in other units (such as °F or
°R), the value of CEM43Tx will be
different if its unit does not contain the unit of the temperature.
In the assumed mathematical form,
R43-T(τ) has no
dimension, which is not scientifically viable.
Moreover, CEM43Tx is
controversial, and has failed to show the local control
characterization of clinical results in soft tissue sarcomas
(26), but was in line with
clinical results for superfi-cial tumors (27). The administered dose of
CEM43T90 for local hyperthermia did not exhibit
an association between dose and clinical outcomes (such as local
remissions, local disease-free survival and overall survival)
(28). It has been calibrated by
in vitro experiments (26),
which are far from the reality of human medicine. Its necrotic
reference at 43°C renders this dose unrealistic, as in most human
hyperthermia treatments such a temperature is not reachable in the
whole tumor. While the high temperature is realized in the
ablation-like locality, the dosing by CEM43Tx was
false (29). The inapplicability
of this in vitro-calibrated dose is echoed in the whole-body
hyperthermia (WBH) application, in which
CEM43T100 is very high (T100
means the complete isothermal heating of the tumor), although the
results are very different from the same dose provided by local
hyperthermia of the tumor lesion (30).
Sometimes, the dose CEM43Tx is
further cumulated by a number of treatments, i.e., 5 repeated
treatments of 90 min each, having a different temperature
definition, but using T90, which is the average
temperature of 90% of the tumor volume (in the case of point
sensors, 90% of the sensors) during the 60 min treatment time
(31) [Equation 7]:
The CEM43Tx in general use depends
on the number of sessions (N), the duration of the nth
session (tn) and of couse Tx is
also time-dependent [Equation 8]:
This cumulation needs to be assessed for the
additive effects of the applied sessions independently of their
repetition frequency. It is likely that a more extended period
between sessions will have a different effect than frequent
repetition, due to many changes in the level of stress proteins and
the proliferation rate of the remaining living part of the tumor,
although these are not considered.
The lack of a consensus on dose is the most
substantial blockade to hyperthermia applications. A further
challenge is that it is almost impossible to measure among standard
conditions; it supposes measuring the temperature. However, the
measurements must describe a map of the distribution, which needs
many measured points in a tumor. This can be done invasively once.
In most publications, the researcher measures the temperature
intraluminally near the tumor. This indirect measurement of tumor
temperature could skew the whole hyperthermia process. Usually, the
intraluminal applications are not precise, as the physiological
conditions (mainly the blood-flow) produce different temperature
there than in the tumor. Equal energy absorption heats the probe in
the lumen to a higher temperature. There is no guarantee that the
lumen is heated at the same energy flux as the tumor. Introducing
the specific absorption rate (SAR, W/kg) parameter over time (such
as in radiation therapy, Gy=J/kg=SAR x time) would be a good dose
option. Intensive surface cooling does not allow the correct energy
dose; energy, which is taken away by cooling, is missing from the
dose. The SAR and the temperature distribution are not identical
(32).
There has been a weak attempt to modify the
CEM43Tx and its cumulation by introducing the
dose TRISE (33-35). TRISE is a custom-made thermal dose
parameter based on T50 and the duration of heating, guessing the
rise in the average temperature (Trise). TRISE
emphasizes the rise in temperature concerning human body
temperature. i.e., 37°C. This supposes that the size of the tumor
does not change during the treatment, and the sensors remain in the
same positions in the tumor. For example, when the treatment time
is unified by every session (90 min), and 5 sessions are in the
protocol with the same 〈T50n〉 (32), then [Equation 9]:
(using the original notations) [Equation 10]:
Which is in a generalized form [Equation 11]:
More preciously [Equation 12]:
where ‘N’ is the overall number of sessions and ‘n’
is the successive number of treatments in the complete cycle of
sessions, ‘tn’ is the duration of the actual
nth session, and 〈T50(τ)〉 is
the actual treatment average over Tx which is the
temperature in x=50% of the monitored sites of the target. The
average treatment, which covers the part of the target in general x
is [Equation 13]:
The Trise(N,tn)
dose (measured in °C) is a definite temperature and differs
entirely from CEM43Tx which is measured in minutes. The
temperature is an intensive thermodynamic parameter, which means
that it characterizes the thermal situation with an average
independent of the mass or volume of the considered system. The
temperature is, in the isothermal case, the same in every smaller
part of the target, while we expect proportionality of the dose
with the volume, i.e., half the volume (mass) would have half the
dose. Here again, the possibility of adding subsequent treatments
forming an overall dose is entirely missing.
Trise(N,tn) is
approaching the SAR on 50% isothermal area of the tumor, and making
great average on the inhomogeneities as well as on the
time-variation of the absorbed energy. The correct dose (absorbed
energy, AE) which transforms Eq.(12) scientifically correct and actually
optimal [Equation 14]:
[14]
Knowing that [Equation 15]:
In the adiabatic approach the average is [Equation
16]:
where ΔT is the temperature increase during the actual session. The
Eq.(
16) is similar, but more
precise than Trise(N,tn) shown
in [Equation 12]. The adiabatic conditions can be ensured by the
well selected absorbing volumes and well controlled incident power.
Systemic and local physiological effects introduce
inaccuracies to the empirical doses in models in vivo,
despite some actual measurements in preclinical research, such as a
randomized canine trial show the significance of
CEM43Tx dose (36). The complete dosing attempts by
CEM43Tx and TRISE are in fact impractical and not
applicable in daily practice, and their formulation is far removed
from the criteria of scientific requirements for dosing.
The thermal effect
Generally, oncological hyperthermia is the result
of energy absorption, which changes the target via chemical,
structural, mechanical and electromagnetic variations (the induced
anthropogenic fever therapies, or inflammatory local heating by
biological effects are not discussed herein). Our topic is limited
only for the energy-intake from outside (mostly electromagnetic)
sources (37). These processes are
constrained and the homeostatic control tries to re-establish the
thermal equilibrium by physiological negative feedback effects,
mainly by the regulation of vasodilatation. There are some other
methods, such as fever production with drugs or biomaterials.
However, the physiological mechanisms are opposite than the case by
energy absorption; herein, the physiological feedback is positive,
inducing the new type of homeostasis. Presently, we deal with only
the energy-absorption based hyperthermic methods, which distort
malignant cells. Energy absorption changes the temperature of the
target in most cases. The temperature can be a tool for
restructuring or merely signaling cell death and may orchestrate a
complex set of molecules acting systemically against
malignancy.
When all the absorbed energy is used for a phase
change, the temperature will be fixed during this transition.
Defining this effect as ‘non-thermal’ (38) is an innacuracy. A set of complex
thermodynamic and bio-electrodynamic interactions is involved in
the process (39), changing
various physical characteristics, such as the chemical potential,
the entropy, the dipole moments; or they may include in chemical
reactions, polarizing molecules, producing an electric current, and
so on.
Hyperthermia is a thermal effect on living
subjects. Consequently, the Arrhenius function as the basis of the
correct dosing (such as was selected for CEM43Tx
too) is a perfect choice (22,40).
The accurate fitting of experiments to the Arrhenius plot in
vitro (41,42) is convincing regarding the thermal
processes. The R-value changes according to the slopes of
the Arrhenius plot. The kink in Arrhenius plot (43), with a sudden change of the slope of
the line, is an excellent basis to fit the activation energies
below and above the kink at a certain temperature, which provided
the value of ‘R’ in [Equations 4 and 7]. However, the
observed kink is an individual process probably connected to the
phase transition. The temperature of the kink is reproducible under
the same conditions and same cell line; however, it changes
depending on the actual complementary chemotherapy (43,44)
or actual cell or tissue (45).
Due to the fundamentally complementary applications of
hyperthermia, this change in the kink is frequent. The kink is not
fixed under preheating conditions (46-49)
and it is sensitive to the dynamism of heat transfer as well
(50); thus, the R-value
has to be adjusted to the actual position of the kink.
The kink in the Arrhenius plot is probably a
lipid-associated phase transition (50-52),
which could lower the activation energy to facilitate changes in
the energy provided (53). The
change in the kink is expected to be responsive to the blood flow
as well (54).
When the kink happens in the Arrhenius plot at
Tc
temperature, and the activation energies are
Ea1 and Ea2 above and below it,
respectively, then the generalization of R in the CEM-like
formulation (55,56) is as follows [Equation 17]:
where T is the absolute temperature, measured in K.
When T≅Tc, Rgen is
constant. We may select Tc as the homeostatic
body temperature, 310 K (37°C), as was selected in the
TRISE proposal. This formulation efficiently introduces
generalized cumulative equivalent minutes concerning
Tc [Equation 18]:
When the activation energies are Ea1
= 365 kcal/mol ≈ 1527 kJ/mol below this point, while above
Ea2 = 148 kcal/mol ≈ 620 kJ/mol, below and above
the kink point, respectively (18,41),
then these values implicate Rgen(<43C)=0.159;
Rgen(≥43C)=0.474, instead of the widely used
R(<43C)=0.25; R(≥43C)=0.5,
respectively. The error is below the robust breakpoint (~36%),
indicating that non-necrotic damage cannot be described accurately
with the standard CEM43°C dose. In in vitro
experiments, x=100% in the Tx(V,t)
function in [Equation 5]. This remarkable deviation occurs as the
kink is artificial. The plot is a curvature in reality and depends
on the spatial-temporal heterogeneity of the process. Thus, the
extrapolated straight line is incorrect in the vicinity of the
transition, e.g., the binding of adenosine triphosphate (ATP) to
myosin subfragment-1 (46,51) or measuring the cytochrome c
reductase activity of liver mitochondrial succinate for the
heterothermic brown antechinus (57,58).
Making the
CEM⎪Tc(t) value scientifically
correct, independent of the measuring units of T temperature
[Equation 19]:
Here, (Tc−T(t))Tc=ΔT(τ)Tcis
free from the dimension (measuring unit) of the temperature, and
Q=constant (when T≅Tc). Due to the high value of
temperature in K, but its relatively small difference from
Tc in this case [Equation 20]:
The Arrhenius graph gives different time doses for
the different points of the target (due to its non-homogeneous
structure); this promotes chemical reactions and lowers the
activation energy (59). In the
case of multiple processes, the so-called ‘apparent activation
energy’ Eaa should be introduced (60) [Equation 21]:
When the pre-exponential factor has a temperature
independent and temperature dependent part, a constant ‘A’
can be separated from the temperature; thus, Eaa
is the independent part of the temperature, and thus (61) [Equation 22]:
kr=ATme−EaaRgT
In practice, it is a rough linear slope fit on the
measured ln(k) vs. (1/T) function, where a deviation
from the slope will refer to differences in the actual chemical
reactions. Of note, a complex chemical reaction, such as cooking
can be described with such apparent activation energies (62).
The Arrhenius curve is most frequently measured
in vitro, where necrotic cell death is considered to be the
dominant thermal effect under cell culture conditions. In cases of
pure thermal necrosis in vitro, the cell membrane is
lethally damaged [e.g., due to protein denaturation (63)], and the damage point changes the
kink of the Arrhenius plot depending on the kind of heating
(64). Even the protein folding
kinetics exhibit an Arrhenius temperature dependence when corrected
for the temperature dependence of protein stability (65) and = trans-membrane protein-lipid
and protein-protein interactions (66).
The Arrhenius mechanism has a more sophisticated
theory, using the variance in the reaction rate by temperature to
study the transition phase of the reaction on the energy of the
barrier (67,68). In this manner, the semi-empirical
Arrhenius equation was rigorously derived from statistical
thermodynamics (69), using the
enthalpy of activation together with the entropy change in the same
process. The transition state of this complex process has been
described (20) and further
developed (70) for cell death,
which approaches practical applications for the thermodynamic
description of the multistep complex biological progression of
interactions. This rigorous thermodynamic explanation has
generalized the thermal dose with improving accuracy possible
(71). Eyring and Polanyi (Eyring
et al, Wynne-Jones and Eyring H, Eyring and Polanyi, Eyring,
and Eyring and Stearn) developed a theoretically well-supported
modification of the Arrhenius plot (68,72-75),
which was developed further in Fig.
6 and can be used in quantum-mechanical chemistry (76).
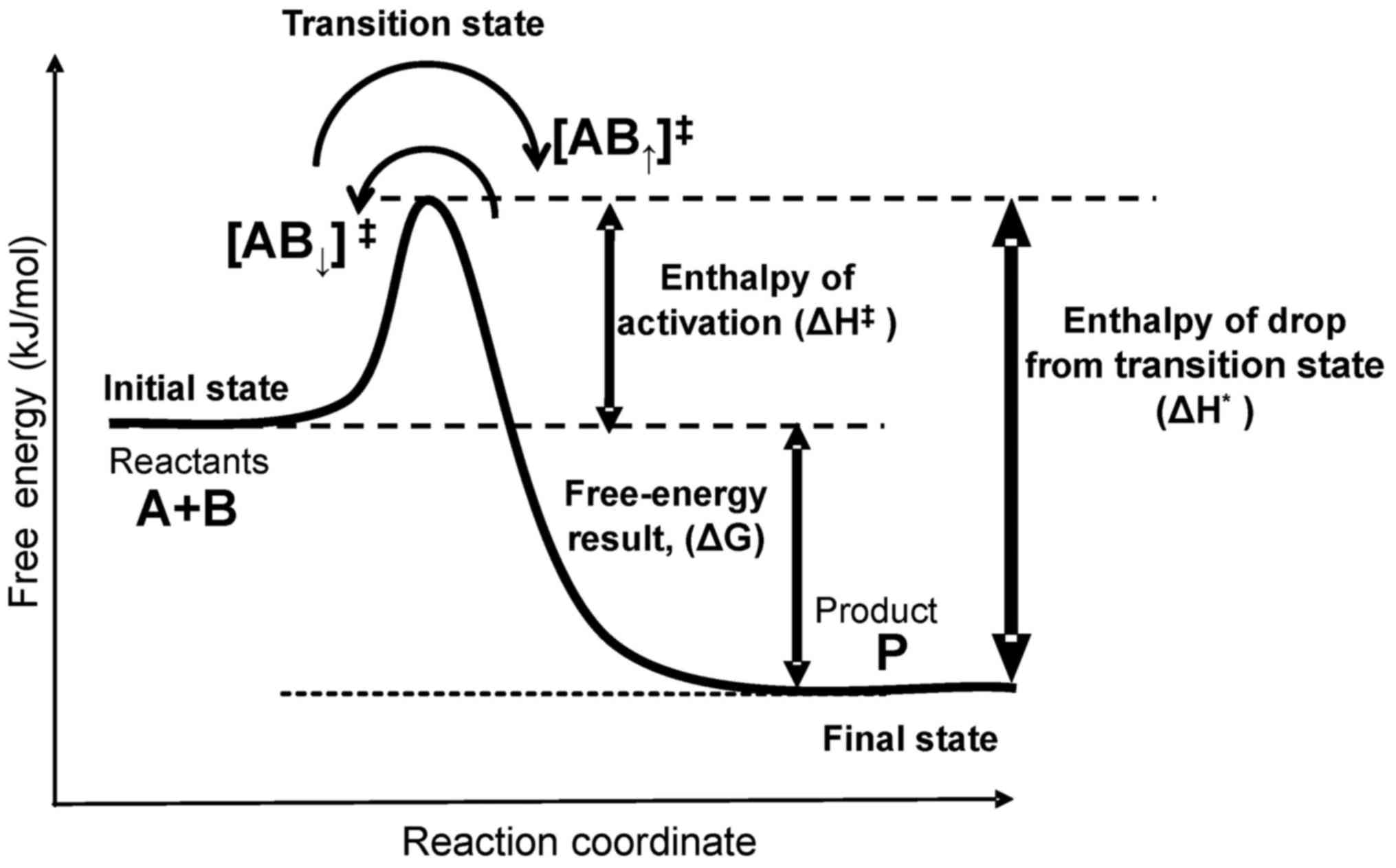
The vital assumption of the transition-state theory
is that the transition state is in equilibrium with the reactants
and products in the state of the activated complex (11).
The Eyring formulation reforms the reaction
coordinates of the conventional empirical Arrhenius plot. The final
product develops steadily from the reactant configuration through a
transition state. This interim phase is a cluster configuration of
the activated transitional complex. In this approach, the reaction
coordinate follows the gradient path of potential energy from the
initial reactants to the final products, e.g., in simple reactions,
the lengths of bonds can be chosen as the reaction coordinate. The
transition state population [Equation 23]:
where ΔG# is the free energy of activation
(transition state), kB is the Boltzmann's and
h is Planck's constant, υ is the vibration frequency of
activated complex and ktr# is
the population of the transition state, and the constants are as
follows [Equation 24]:
kB=Rg6.022·10−23m2kgs2K≅1.38·10−23,h≅6.626·10−23m2kgs
Note that the factor (kBThv)is the ratio of the actual thermal
and quantum-mechanical energy.
From these, Eyring's expression is formally similar
to that of Arrhenius [Equation 25]:
Where ‘κ’ is the transmission coefficient;
it is the probability of oscillation of the activated complex in
the transition state leading to a product. The difference, however,
is essential: While the Arrhenius plot describes an experimental
macroscopic rate constant for the entire transformation process,
the Eyring plot deals with microscopic transitions as fundamental
steps.
Due to the thermodynamic conditions [Equation
26]:
ΔG#=ΔH#−TΔGS#
where ΔS# and ΔH# are the
entropy and enthalpy of activation. For simplicity, we use the
molar values of the extensive thermodynamic parameters [Equation
27]:
Using [Equations 25 and 26], we get the following
[Equation 28]:
A comparison of [Equations 28 with 1] makes the
pre-exponential frequency factor and the activation energy in
empirical Arrhenius function scientifically accurate [Equation
29]:
This result provides an essential explanation for
the theoretical background of the pre-exponential factor and the
activation energy. The ΔH‡ enthalpy is the kind
of energy manifested in a transition state, while the
ΔS‡ entropy represents the energy ‘trapped’
during the interactions.
The Eyring and Arrhenius plots are similar to the
fitting of the curves does not differ in the physiological range
(77); however, the slope and
intercepts have different meanings in Fig. 7. The significant difference is that
while the ordinate shows the logarithm of the reaction rate ‘k’ in
the Arrhenius plot, in the Eyring plot, the ordinate has a
temperature dependent addition. The superiority of the Eyring model
is its theoretical background compared to the empirical Arrhenius
model. The central fact that we can use in hyperthermia is that the
pre-exponential factor of the Arrhenius plot is entropy dependent.
The entropy abruptly jumps during phase transitions, with immediate
changes to the chemical structure, which is the essential
requirement of hyperthermia.
The Arrhenius parameters (Ea and
A) are functionally connected empirically (78) [Equation 30]:
Eα≅2.61⋅103ln(A)+2.62⋅104
Or [Equation 31]:
ln(A)≅3.832⋅10−4Eα−10.042
while others (
79,
80) have slightly different values
[Equation 32]:
Eα≅2.63⋅103ln(A)+2.46⋅104
Or [Equation 33]:
ln(A)≅3.8⋅10−4Eα−9.36
The linear plots of the Arrhenius parameters
[Equations 30, 31, 32, 33) are arithmetically given the same linear
dependence of the molar entropy and molar enthalpy due to the
Eyring connections, such as seen below:
If, due to [Equation 29] the below are obtained
[Equation 34]:
Eα=H‡≅cln(A)+d
(c and d are constants) and [Equation
35]:
where q is constant. In consequence [Equation 36]:
where a and b are constants.
It is indeed observed. A collection of data on
molar entropies and enthalpies are found in numerous irreversible
thermal denaturalization references; a linear dependence can be
seen between the change in molar values (81).
Hence, in case of the processes collected in, the
following are obtained [Equation 37]:
ΔS=αΔH+b
where b=-327.5 [J/mol/K] and a=0.003147 [1/K]; others (
82) measure b′=-271.7 [J/mol/K];
a′=0.0030395 [1/K] according to the best fit of the line.
Using the thermodynamical equivalence in [Equation
26] the following are obtained [Equation 38]:
This expression offers the ability to control the
accuracy [Equation 39]:
and [Equation 40]:
The above-calculated temperatures fit the
experimental conditions. From this, the change in the free energy
is as follows [Equation 41]:
ΔG≅104,067[J/mol]
and [Equation 42]:
ΔG′≅89,389[J/mol]
which is in the range of the usual experimental expectations.
The main consequence of this observation is a clear
picture of robustly used energy utilization for chemical changes
and differs from the process which leads to an increase in the
temperature only.
These processes probably represent different
molecular reactions, which require further investigations. This
shows that the absorbed energy is utilized for different purposes,
not only for raising the temperature. When we intend to change the
structure, all the energy components (the chemical reactions, the
mechanical properties, and so on) require energy, and the rest will
be distributed equally to increase the average kinetic energy of
the part of the system. Consequently, the energy that is not used
for particular purposes will ‘invested into the pool’ and will
increase the temperature. The increasing temperature represents
energy that has no specialized tasks, and thus in this regard, it
is wasted energy.
Furthermore, we know another linear expression of
molar entropy for the temperature adaptation of enzymes (83) [Equation 43]:
where and K (sec−1) = (Vmax/mg of
enzyme) × (molecular weight) × (10−3 mmol/µmol) × (1
min/60 sec), where the molecular weight of the enzyme is expressed
in mg/mmol.
The connections between the activation parameters
are observed in cases of muscle-type lactate dehydrogenase,
D-glyceraldehyde-3phosphate-dehydrogenase, and muscle glycogen
phosphorylase b.
To verify the effect of hyperthermia, thermal
damage is measured in multiple experiments. CEM usually
character-izes the damage dependent fit to the Arrhenius plot and
accurately fits the Arrhenius plot in vitro (41,43).
According to [Equation 7], the proportional fitting value R
depends on the rate of thermal destruction. Since this destruction
rate varies according to tissue type, R is not constant at
all (84).
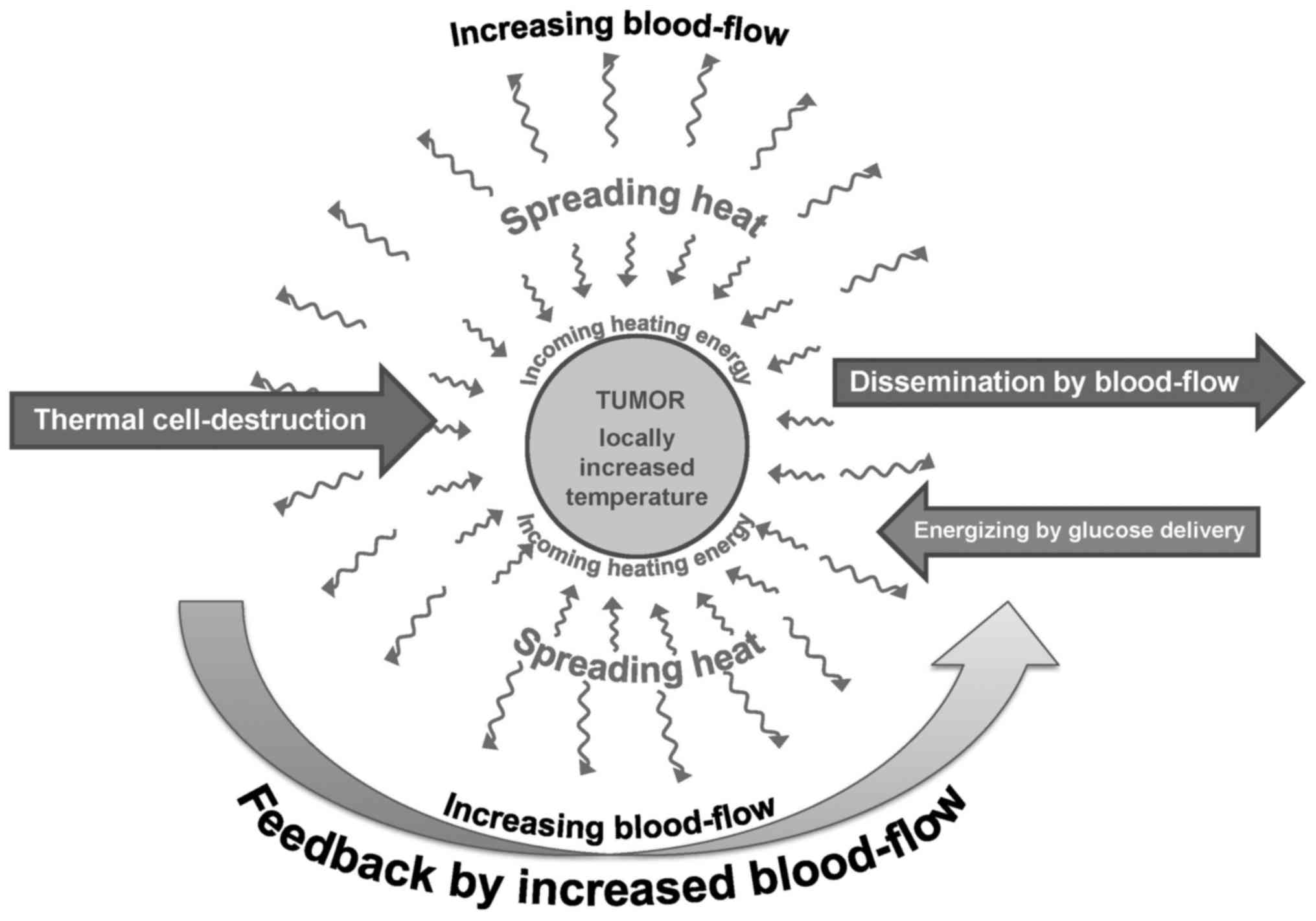
Concept: Dose model of modulated
electro-hyperthermia
The variability of destruction, as well as the
challenge of the previously described competitive effects of
thermal damage and blood flow, together with intensified
dissemination, need another concept than the pure thermal
destruction demonstrated in vitro. The thermal process has
to be sufficient for the disruption of malignant cells and for
sensitizing complementary therapies; however, along with these
effects it must not increase the blood flow to a high degree, as
this has the deleterious effects of increasing the tumor's nutrient
supply and the dissemination of malignant cells, as shown in
Fig. 8.
A new type of hyperthermia appears to have solved
this challenge: Modulated electro-hyperthermia (mEHT, trade name
oncothermia) (79). This method is
devoted to using non-temperature dependent thermal effects, which
are capable of triggering apoptotic processes by specific molecular
processes. We disapprove of the concept of the isothermal heating
of the whole tumor mass, avoid the controversial effect which is
caused by the feedback of thermal homeostasis, which uses the
non-linear control of blood-flow. The energy absorption by the
individual malignant cells uses the energy where it is necessary,
to initiate apoptotic signal transductions. In consequence, the
measured temperature and the stimulated blood-flow are mild
(85), but the local control and
the overall survival are both increased (86). In this manner, mEHT leads to
selective heterogenic heating, genuinely breaking the homogenous,
isothermal concept.
The mEHT method uses the biophysical differences
between healthy and malignant cells for selection of its action,
precisely heating in a nanoscopic range and igniting molecular
reactions (87). The selection
exploits the character of malignant cells, which indeed differ from
their healthy counterparts. Healthy cells are in a communicative
network, maintaining the complexity of a well-controlled system,
while malignant cells are mostly autonomic, having lost their
‘social’ connections with other cells, and fighting for with every
other cell nutrients, irrespective of their health status. The
existence of the network categorizes cells as connected or
non-connected (88). Malignant
transformation can be regarded as a phase transformation (89), as cells lose their multicellular
behavior (90) transforming the
highly complex network into a set of individual cells (91,92).
This process is similar to reverse evolution (atavism) (93). However, it is different from
prokaryotes. These cells are well-developed eukaryotes with
complete genetic content, although they have lost their collective
complexity, and their mitochondria are not able to supply the
enormous energy demand for permanent proliferation.
The consequences of malignant differences indeed
provide the possibility to distinguish them from healthy cell
arrangements (94). This
differentiation is based on the contents of the extracellular
aqueous electrolyte. The higher metabolism of malignant cells needs
a robust amount of glucose for ATP production, which is measurable
by positron emission tomography (95). In cancer cells, ATP production is
predominantly performed by simple anaerobic glycolysis instead of
mitochondrial phosphorylation. This rapid, intense process produces
lactate which, together with the higher transport of other ionic
species, considerably increases the ionic conductivity of the
electrolyte in the extracellular matrix of the tumor. An applied
radiofrequency (RF) current prefers flowing through the low
resistance tumor than the healthy environment. This effect is
measurable by RF current density imaging (96). The RF current predominantly flows
in the extracellular electrolyte. Its energy-absorption creates an
active temperature gradient through the membrane (97).
This tumor selection is accompanied by a cellular
difference, making the selection microscopic. In the mEHT method,
the overall physiologic feedback loops are not promoted by massive
general temperature increase of the targeted volume; mEHT functions
as mild hyperthermia macroscopically, while it functions as extreme
hyperthermia microscopically for malignant cells. Malignant cells
are autonomic and break their intercellular communications, i.e.,
contacts via adherent proteins and junctions mostly vanish. This
difference in the structure of the extracellular environment in the
near vicinity of cells (98)
renders them distinguishable by their dielectric permeability
(99,100), for which the applied RF current
flow is discriminatory. This is a well-developed diagnostic method
(101) that is applied in
mammography (102).
Furthermore, the complete pattern of the malignant
tissue differs from the pattern of healthy tissue, which is used
for pathological image recognition in biopsy samples. The
pathological pattern modifies the spatiotemporal interactions of
the cells, which is not a static pattern but dynamically acts via
intercellular interactions. These dynamic relations produce a noise
of homeostatic equilibrium, which is measured as a peculiar signal
(103,104). This noise differs in malignancy
versus healthy tissue (104) and
is measurable by the RF current (105). The noise difference is the basis
for the applied modulation on the RF carrier. The modulation is one
of the important features of mEHT (oncothermia) method (106). The modulation is an information
delivery to the malignant lesion. The applied time-fractal has such
autocorrelation time-lags that well fits to the apoptotic
excitation processes and also may reconstruct the broken
E-cadherin-beta-catenin cellular connections (107), in repeated independent
measurement as well (108).
Technically mEHT couples the electromagnetic energy
by high-precision impedance matching (patented), which renders such
tight coupling similar to it galvanic. Reflection at 150 W incident
is <1% (1 W) in the maximal output of oncothermia device. The
conventional hyperthermia devices use 10 times more power than
mEHT; however, most of that vanishes by various energy losses
(radiation to the air, high energy reflection, heating the
electronic parts, etc.). Consequently, they must measure the
temperature in the target having idea about the absorbed energy
there. The innovative tight coupling allows to use the energy as
dose of the mEHT treatment (85).
The above-mentioned selection steps guide energy
delivery; using β-dispersion involving bound water on the membrane
(109,110). The broad range of β-dispersion
has a part denoted by δ, (111),
which is primarily selective for transmembrane proteins. This
effect indices real energy absorption, which happens at clusters of
transmembrane proteins (112-114). All these publications above show
the excellent selectivity of the mEHT method, acting on the
membrane rafts of the malignant cells, while do not harm any
healthy cells, having properties which are well distinguishable by
the above-described biophysical factors from the malignant cells
(87). The mEHT makes the same
apoptosis as conventional hyperthermia does but in lower
temperatures by 3°C (115,116),
which is the consequence of the absorption of the energy in
transmembrane proteins in the rafts.
Selection and energy absorption by a modulated RF
current induce cell destruction beyond simple thermal effects. The
in vitro research shows the absolute differences of mEHT
from the conventional heating like water-bath or simple capacitive
coupling (108,115). The in vitro proven
increased efficacy has been supported by in vivo research
(117) and continues to prove the
feasibility in preclinical (118)
and clinical applications (119)
as well.
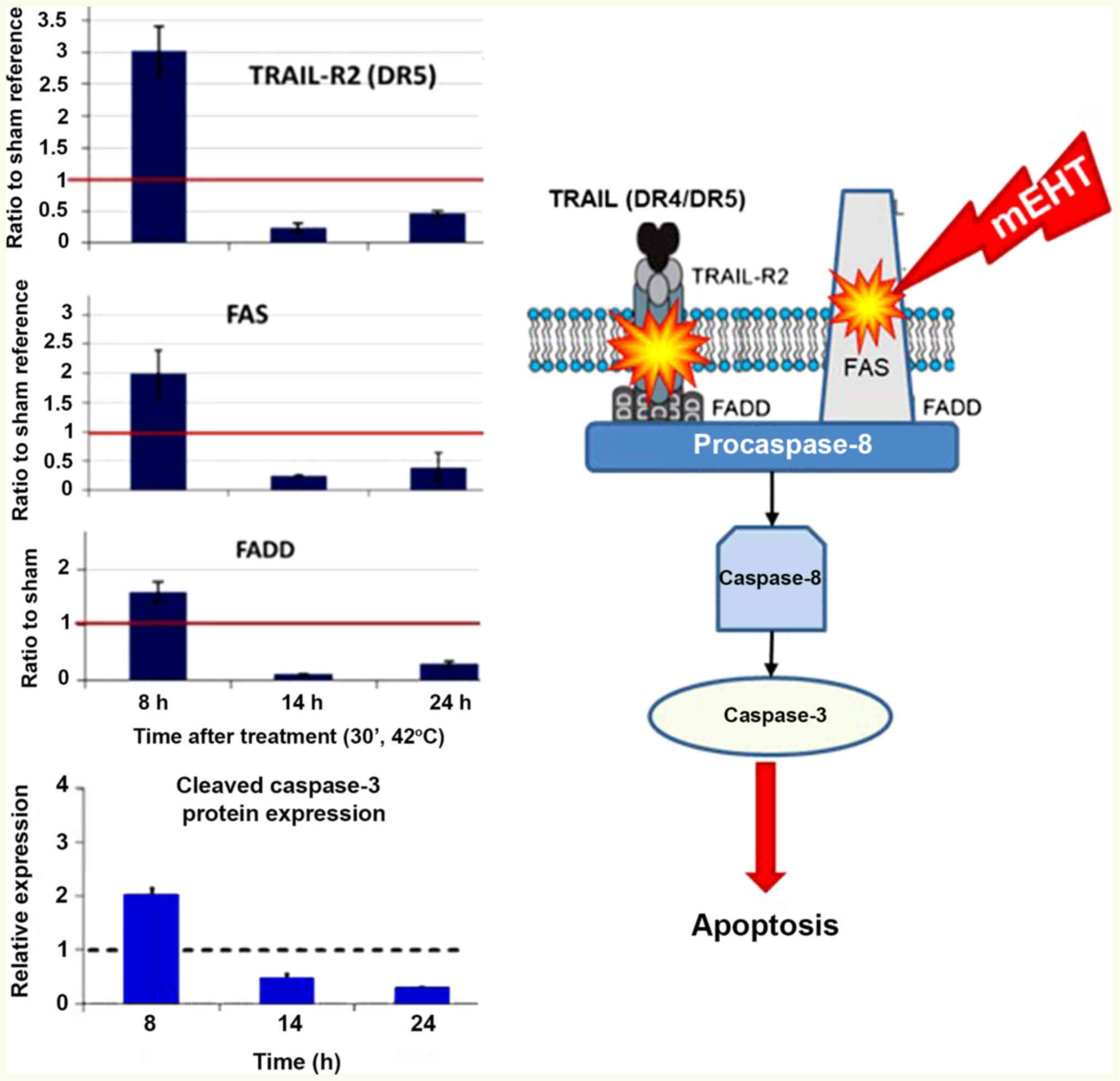
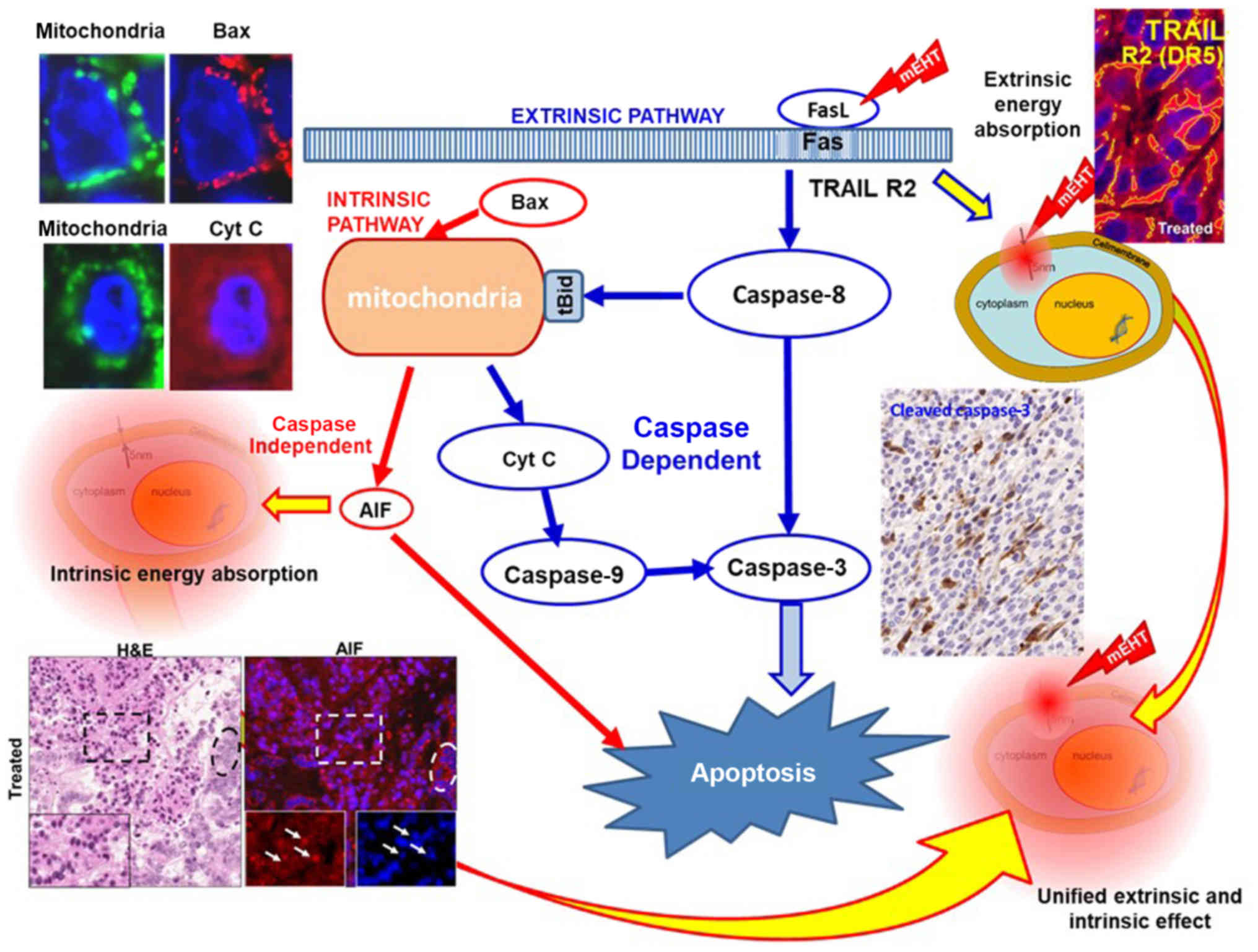
The absorbed energy induces a particular apoptotic
process in transmembrane proteins (113), which energy is absorbed by the
membrane rafts (structure of transmembrane proteins). This energy
promotes the extrinsic pathway of apoptosis through the
TRAIL-FAS-FADD complex, leading to cleavage of executor caspase-3
and induction of the apoptotic process, as shown in Fig. 9 (120). Additionally, the activation of
caspase-8 could trigger intrinsic pathways together with the
cell-wide spread of heating energy. These intrinsic pathways
include caspase-independent [activate apoptosis-inducing factor
(AIF) (121)] and
caspase-dependent apoptosis through cytochrome c (122). Furthermore, the pro-apoptotic
cell death-related gene network (such as EGR1, JUN and CDKN1A) in
induced, as well as the cryoprotective gene network (HSPs)
(116). Various pathways are
united in the final mechanism of action (Fig. 10).
The destruction of the malignant cell is dominantly
apoptotic by the above signal excitations (120) developing a damage-associated
molecular pattern (DAMP) (121),
is the basis of immunogenic cell-death (ICD) (122). These processes prepare antigen
recognition cells to produce helper and killer T-cells with direct
recognition of the malignant cells over the body, finding the
disseminated cells and distant metastases, (abscopal effect)
(123,124).
This targeting of the extrinsic pathway requires
much less energy than heating the complete mass of the tumor, and
furthermore, it is a direct apoptosis induction, which is not the
case in the isothermal heating. The properly selected energy
absorption is the reason why mEHT uses considerably less energy
than conventional hyperthermia (125), while its results are showing
significant improvement of both the local control and survival time
(86).
Thermally activated non-necrotic cell-killing has a
point of no return, where the process becomes irreversible, and the
cell is committed to die. One of the pathways is BAX-mediated pore
formation on mitochondria and the release of cytochrome c.
Apoptosis and necrotic cell death are complex processes involving
numerous chemical reactions and required a long period of time to
be completed (126). The
apoptotic signals begin the process, which is at the beginning,
reversible. There are some points (depending on the signaling
pathway) which are the ‘points of no return’ from where the process
automatically continues and finishes by positive feedback
constraint. In principle, the final phagocytosis of apoptotic
bodies could be 48 h after the process has commenced.
One of the characteristic points of no return is
the release of cytochrome c from the mitochondria (127), which usually takes 4 h after the
initial apoptotic signal. Apparent activation energies associated
with protein dynamics show relatively simple straight-line
Arrhenius plots, so deviations from the single reaction plot are
acceptable (128). In most
reactions in living systems, Arrhenius plots are linear (no kink)
below 42°C, e.g., in the mitochondrial membrane (54,129) and BAX-mediated pore formation
(130,131) which is connected to cytochrome
c (132,133), the appearance of which is one of
the points of no return. Essential variations in cell polarity
(134), enzymatic reactions
(135), signaling pathways
(136), or the activation of the
hsp27/p38MAPK stress pathway (137) could help destroy or modify
cancerous tissues.
A single Eaa can describe these
processes as the kink of the Arrhenius plot is outside the
investigated temperature interval. Using the Eaa
apparent activation energy in complex reaction-kinetic processes of
apoptosis can be formally converted to the apparent molar enthalpy
and molar entropy. The entropy shows the energy part, which is
trapped in the chemical and structural changes caused by the
treatment. For dosing, we have to choose a parameter characterizing
the process of non-necrotic cell killing.
The Eyring (Arrhenius experiment) plots show the
possibility of the CEM-like behavior of the dose, as indicated
earlier (20,55). However, the difference from the
flawed CEM43°CTx is remarkable. No kink is considered in
any of the curves of the various temperature dependences of various
protein changes, only the slope (molar enthalpy) and molar entropy
involved in the pre-exponential factor are used as proposed
(20,55). This has specific disadvantages;
however, we have to be sure that only apoptosis is characterized,
which involves the actually chosen protein and indicates a definite
commitment to apoptosis. This protein could be cytochrome c,
cleaved caspase-3 or AIF. The signal transfer to apoptosis can
occur through various ways.
The signal transduction pathways of apoptosis are
mixed and produce a defined result. Thus, we have to use the same
concept as that used for ionizing radiation. There, we know that
the dominant effect breaks the strands of DNA, which anyway follows
Arrhenius plot (138). Heat may
also break DNA as shown by its Arrhenius behavior (139). With ionizing radiation, no
calculations are made regarding the kind of damage (how many and
which strands are damaged); the only point is the measurable
result, which is proportional to the applied energy. By targeting
breaks in DNA, isodose energy is used, assumed that all malignant
cells have the same power to destroy their DNA strands. All the
other absorbed energy, which makes heat or destroys parts of
healthy cells, is regarded as a side-effect. The isodose condition,
of course, has many side-effects, as malignant cells are only
slightly selected under isodose conditions. The mEHT method enables
the more precise selection since the target has self-selection
mechanisms orienting the energy to the places where it acts
optimally, which is measurable (113,120-122,140). The efficacy of energy delivery
also must be optimal, which has been shown for mEHT (125). The mEHT method is highly
personalized (55,141) and thus minimizes adverse effects.
Consequently, the dose of mEHT could be the same as for ionizing
radiation, with the energy defined as J/kg (Gy) or Ws/kg.
The above considerations are valid for single shot
treatments. However, this is not sufficient, as clinical
applications always use multiple sequential treatments. A series of
sessions is applied clinically, so ‘fractional heating’ can be
dosed. This requires clarification regarding the equilibrium of
permanent cell death and the fresh round of cell proliferation, as
well as the possibility of reverse chemical reactions. This problem
overshadows fractional radiotherapy applications (142,143), as the repair of damaged DNA
modifies the results of fractional therapy (144). In our fractional treatment
method, this problem is less critical as apoptosis induced via the
intrinsic and extrinsic ways is complete, no DNA repair is
possible, and only the further proliferation of malignant cells
leads to regrowth of the tumorous lesion. The critical result is
that proliferation is suppressed in cells not destroyed in the
target, measured by the Ki67 proliferation index (145).
Taken together with the molecular changes, the
treatment capable of sensitizing the tumor to radio- (146) and chemo- (147) therapies, solving the challenge of
the significant and controversial vasodilation induced by the
conventional hyperthermia.
In conclusion, the appropriate dose of oncological
hyper-thermia has to be the well-known energy-based concept, Gy
(=J/kg). This dose is appropriate for the complex non-ionizing
radiation process and also unites the complete radiation field
(together with ionizing radiation) around the same dose
control.
Funding
AMS is grateful for the support of the Hungarian
Competitiveness and Excellence Program grant
(NVKP_16-1-2016-0042).
Availability of data and materials
Not applicable.
Authors' contributions
SYL, GPS and AMS were involved in the conception
and design of the study and worked together on drafting, revising
and finalizing it. All authors have read and approved the final
manuscript.
Ethics approval and consent to
participate
Not applicable.
Patient consent for publication
Not applicable.
Competing interest
The authors declare that they have no competing
interests.
Acknowledgments
Not applicable.
References
|
1
|
Nielsen OS, Horsman M and Overgaard J: A
future for hyper-thermia in cancer treatment. Eur J Cancer.
37:1587–1589. 2001. View Article : Google Scholar : PubMed/NCBI
|
|
2
|
van der Zee J: Heating the patient: A
promising approach. Ann Oncol. 13:1173–1184. 2002. View Article : Google Scholar : PubMed/NCBI
|
|
3
|
Roussakow S: The History Of Hyperthermia
Rise And Decline Hindawi Publishing Corporation. Conference Papers
in Medicine 2013; pp. 34280272013;
|
|
4
|
Oncology Encyclopedia: 2008, MedicineNet
Hyperthermia definition, Answers. http://www.answers.com/topic/hyper-thermia.
Accessed May 23, 2018.
|
|
5
|
Medicine.net: 2008, Hyperthermia
definition. http://www.medterms.com/script/main/art.asp?articlekey=3848.
Accessed May 23, 2018.
|
|
6
|
National Cancer Institute Hyperthermia
definition. http://www.cancer.gov/about-cancer/treatment/types/surgery/hyperthermia-fact-sheet.
Accessed May 23, 2018.
|
|
7
|
Wikipedia: Hyperthermia definition.
https://en.wikipedia.org/wiki/Hyperthermia_therapy.
Accessed May 23, 2018.
|
|
8
|
Medical Dictionary Hyperthermia
definition. http://medical-dictionary.thefreedictionary.com/hyperthermia.
Accessed May 23, 2018.
|
|
9
|
The Americal Cancer Society: Hyperthermia
definition. http://www.cancer.org/treatment/treatmentsandsideeffects/treat-menttypes/hyperthermia.
Accessed May 23, 2018.
|
|
10
|
Arrhenius S: On the reaction rate of the
inversion of non-refined sugar upon souring. Z Phys Chem.
4:226–248. 1889.
|
|
11
|
Peleg M, Normand MD and Corradini MG: The
Arrhenius equation revisited. Crit Rev Food Sci Nutr. 52:830–851.
2012. View Article : Google Scholar : PubMed/NCBI
|
|
12
|
Pollak E and Talkner P: Reaction rate
theory: What it was, where is it today, and where is it going.
Chaos. 15:0261162005. View Article : Google Scholar
|
|
13
|
Thomson WH: Quantum mechanical transition
state theory and tunneling corrections. J Chem Phys. 110:4221–4231.
1999. View Article : Google Scholar
|
|
14
|
Urano M: Thermochemotherapy: From in vitro
and in vivo experiments to potential clinical application.
Hyperthermia and Oncology. Urano M and Douple E: VSP Utrecht;
Tokyo: pp. 169–204. 1994
|
|
15
|
Lin R, Chang DC and Lee YK: Study of
temperature effect on single-cell fluid-phase endocytosis using
micro cell chips and thermoelectric devices. 14th International
Conference on Miniaturized Systems for Chemistry and Life Sciences;
3-7 October 2010; Groningen. pp. 962–965. 2010
|
|
16
|
Rosemeyer H, Körnig E and Seela F:
Dextran-linked purine nucleosides as substrates and inhibitors of
adenosine deaminase. Eur J Biochem. 127:185–191. 1982. View Article : Google Scholar : PubMed/NCBI
|
|
17
|
Antov Y, Barbul A, Mantsur H and
Korenstein R: Electroendocytosis: Exposure of cells to pulsed low
electric fields enhances adsorption and uptake o. macromolecules =
Biophys J. 88:2206–2223. 2005.
|
|
18
|
Dewey WC, Hopwood LE, Sapareto SA and
Gerweck LE: Cellular responses to combinations of hyperthermia and
radiation. Radiology. 123:463–474. 1977. View Article : Google Scholar : PubMed/NCBI
|
|
19
|
O'Neill DP, Peng T, Stiegler P, Mayrhauser
U, Koestenbauer S, Tscheliessnigg K and Payne SJ: A three-state
mathematical model of hyperthermic cell death. Ann Biomed Eng.
39:570–579. 2011. View Article : Google Scholar
|
|
20
|
Szasz A and Vincze G: Dose concept of
oncological hyper-thermia: Heat-equation considering the cell
destruction. J Cancer Res Ther. 2:171–181. 2006. View Article : Google Scholar
|
|
21
|
Jones E, Thrall D, Dewhirst MW and
Vujaskovic Z: Prospective thermal dosimetry: The key to
hyperthermia's future. Int J Hyperthermia. 22:247–253. 2006.
View Article : Google Scholar : PubMed/NCBI
|
|
22
|
Dewhirst MW, Viglianti BL, Lora-Michiels
M, Hanson M and Hoopes PJ: Basic principles of thermal dosimetry
and thermal thresholds for tissue damage from hyperthermia. Int J
Hyperthermia. 19:267–294. 2003. View Article : Google Scholar : PubMed/NCBI
|
|
23
|
Dewey WC: Arrhenius relationships from the
molecule and cell to the clinic. Int J Hyperthermia. 10:457–483.
1994. View Article : Google Scholar : PubMed/NCBI
|
|
24
|
Perez CA and Sapareto SA: Thermal dose
expression in clinical hyperthermia and correlation with tumor
response/control. Cancer Res. 44(Suppl 10): 4818s–4825s.
1984.PubMed/NCBI
|
|
25
|
Sapareto SA and Dewey WC: Thermal dose
determination in cancer therapy. Int J Radiat Oncol Biol Phys.
10:787–800. 1984. View Article : Google Scholar : PubMed/NCBI
|
|
26
|
Maguire PD, Samulski TV, Prosnitz LR,
Jones EL, Rosner GL, Powers B, Layfield LW, Brizel DM, Scully SP,
Harrelson JM, et al: A phase II trial testing the thermal dose
parameter CEM43 degrees T90 as a predictor of response in soft
tissue sarcomas treated with pre-operative thermoradiotherapy. Int
J Hyperthermia. 17:283–290. 2001. View Article : Google Scholar : PubMed/NCBI
|
|
27
|
Dewhirst MW, Vujaskovic Z, Jones E and
Thrall D: Re-setting the biologic rationale for thermal therapy.
Int J Hyperthermia. 21:779–790. 2005. View Article : Google Scholar : PubMed/NCBI
|
|
28
|
de Bruijne M, van der Holt B, van Rhoon GC
and van der Zee J: Evaluation of CEM43 degrees CT90 thermal dose in
superficial hyperthermia: A retrospective analysis. Strahlenther
Onkol. 186:436–443. 2010. View Article : Google Scholar : PubMed/NCBI
|
|
29
|
Assi H: A New CEM43 Thermal Dose Model
Based On Vogel - Tammann-Fulcher Behaviour in Thermal Damage
Processes. Ryerson University; Toronto: 2009
|
|
30
|
Thrall DE, Prescott DM, Samulski TV,
Rosner GL, Denman DL, Legorreta RL, Dodge RK, Page RL, Cline JM,
Lee J, et al: Radiation plus local hyperthermia versus radiation
plus the combination of local and whole-body hyperthermia in canine
sarcomas. Int J Radiat Oncol Biol Phys. 34:1087–1096. 1996.
View Article : Google Scholar : PubMed/NCBI
|
|
31
|
Franckena M: Hyperthermia for the
Treatment of Locally Advanced Cervix Cancer. Erasmus University;
Rotterdam: 2010
|
|
32
|
Van der Zee J: Radiotherapy and
Hyperthermia in Cervical Cancer, ESTRO/TMH, presentation. Mumbai:
March 2–2005
|
|
33
|
Franckena M, Fatehi D, de Bruijne M,
Canters RA, van Norden Y, Mens JW, van Rhoon GC and van der Zee J:
Hyperthermia dose- effect relationship in 420 patients with
cervical cancer treated with combined radiotherapy and
hyperthermia. Eur J Cancer. 45:1969–1978. 2009. View Article : Google Scholar : PubMed/NCBI
|
|
34
|
Schooneveldt G, Bakker A, Balidemaj E,
Chopra R, Crezee J, Geijsen ED, Hartmann J, Hulshof MC, Kok HP,
Paulides MM, et al: Thermal dosimetry for bladder hyperthermia
treatment. An overview Int J Hyperthermia. 32:417–433. 2016.
View Article : Google Scholar
|
|
35
|
Fotopoulou C, Cho CH, Kraetschell R,
Gellermann J, Wust P, Lichtenegger W and Sehouli J: Sehoul:
Regional abdominal hyperthermia combined with systemic chemotherapy
for the treatment of patients with ovarian cancer relapse: Results
of a pilot study. Int J Hyp. 26:118–126. 2009. View Article : Google Scholar
|
|
36
|
Thrall DE, LaRue SM, Yu D, Samulski T,
Sanders L, Case B, Rosner G, Azuma C, Poulson J, Pruitt AF, et al:
Thermal dose is related to duration of local control in canine
sarcomas treated with thermoradiotherapy. Clin Cancer Res.
11:5206–5214. 2005. View Article : Google Scholar : PubMed/NCBI
|
|
37
|
Blank M and Goodman R: Electromagnetic
fields stress living cells. Pathophysiology. 16:71–78. 2009.
View Article : Google Scholar : PubMed/NCBI
|
|
38
|
Giuliani L and Soffritti M: Non-Thermal
Effects And Mechanisms Of Interaction Between Electromagnetic
Fields and Living Matter. An ICEMS Monograph; National Institute
for the Study and Control of Cancer and Environmental Diseases
‘Bernardino Ramazzini’. 5. Fidenza Publication; Bologna: 2010
|
|
39
|
Vincze G and Szasz A: Critical analysis of
the thermodynamics of reaction kinetics. J Adv Phys. 10:2538–2559.
2015. View Article : Google Scholar
|
|
40
|
Dewey WC: Arrhenius relationships from the
molecule and cell to the clinic. Int J Hyperthermia. 25:3–20. 2009.
View Article : Google Scholar : PubMed/NCBI
|
|
41
|
Lindholm CE: Hyperthermia and Radiotherapy
PhD Thesis. Lund University; Malmö: 1992
|
|
42
|
Hafström L, Rudenstam CM, Blomquist E,
Ingvar C, Jönsson PE, Lagerlöf B, Lindholm C, Ringborg U, Westman G
and Ostrup L; Swedish Melanoma Study Group: Regional hyperthermic
perfusion with melphalan after surgery for recurrent malignant
melanoma of the extremities. J Clin Oncol. 9:2091–2094. 1991.
View Article : Google Scholar
|
|
43
|
Bhowmick P, Coad JE, Bhowmick S, Pryor JL,
Larson T, De La Rosette J and Bischof JC: In vitro assessment of
the efficacy of thermal therapy in human benign prostatic
hyperplasia. Int J Hyperthermia. 20:421–439. 2004. View Article : Google Scholar : PubMed/NCBI
|
|
44
|
Urano M and Douple E: Chemopotentiation by
Hyperthermia. Hyperthermia in Oncology. 4. VSP Utrecht; Tokyo: pp.
1731994
|
|
45
|
Digel I, Maggakis-Kelemen Ch, Zerlin KF,
Linder P, Kasischke N, Kayser P, Porst D, Temiz Artmann A and
Artmann GM: Body temperature-related structural transitions of
monotremal and human hemoglobin. Biophys J. 91:3014–3021. 2006.
View Article : Google Scholar : PubMed/NCBI
|
|
46
|
Lindegaard JC: Winner of the Lund Science
Award 1992 Thermosensitization induced by step-down heating. A
review on heat-induced sensitization to hyperthermia alone or
hyperthermia combined with radiation. Int J Hyperthermia.
8:561–586. 1992. View Article : Google Scholar : PubMed/NCBI
|
|
47
|
van Rijn J, van den Berg J, Wiegant FA and
van Wijk R: Time-temperature relationships for step-down heating in
normal and thermotolerant cells. Int J Hyperthermia. 10:643–652.
1994. View Article : Google Scholar : PubMed/NCBI
|
|
48
|
Henle KJ and RotiRoti JL: Response of
cultured mammalian cells to hyperthermia. Hyperthermia and
Oncology. Urano M and Douple E: 1. VSP, Utrecht; Tokyo: pp. 57–82.
1988
|
|
49
|
Konings AW: Interaction of heat and
radiation in vitro and in vivo. Thermo-radiotherapy and
Thermo-chemotherapy Biology, Physiology and Physics. 1.
Seegenschmiedt MH, Fessenden P and Vernon CC: Springer Verlag;
Berlin: pp. 89–102. 1995
|
|
50
|
Hasegawa T, Gu YH, Takahashi T, Hasegawa T
and Yamamoto I: Enhancement of hyperthermic effects using rapid
heating. Thermotherapy for Neoplasia, Inflammation, and Pain.
Kosaka M, Sugahara T and Schmidt KL: Springer Verlag; Tokyo-Berlin:
pp. 439–444. 2001, View Article : Google Scholar
|
|
51
|
Biosca JA, Travers F and Barman TE: A jump
in an Arrhenius plot can be the consequence of a phase transition.
The binding of ATP to myosin subfragment 1. FEBS Lett. 153:217–220.
1983. View Article : Google Scholar : PubMed/NCBI
|
|
52
|
Watson K, Bertoli E and Griffiths DE:
Phase transitions in yeast mitochondrial membranes. The effect of
temperature on the energies of activation of the respiratory
enzymes o. Saccharomyces cerevisiae = Biochem J. 146:401–407.
1975.
|
|
53
|
Szigeti, GyP, Szasz O and Hegyi G:
Personalised dosing of hyperthermia. J Cancer Diagn. 1:1072016.
View Article : Google Scholar
|
|
54
|
Erdmann B, Lang J and Seebass M:
Optimization of temperature distributions for regional hyperthermia
based on a nonlinear heat transfer model. Ann NY Acad Sci.
858:36–46. 1998. View Article : Google Scholar
|
|
55
|
Vincze G, Szasz O and Szasz A:
Generalization of the thermal dose of hyperthermia in oncology.
Open J Biophys. 5:97–114. 2015. View Article : Google Scholar
|
|
56
|
Pearce JA: Comparative analysis of
mathematical models of cell death and thermal damage processes. Int
J Hyperthermia. 29:262–280. 2013. View Article : Google Scholar : PubMed/NCBI
|
|
57
|
Geiser F and McMurchie EJ: Arrhenius
parameters of mitochondrial membrane respiratory enzymes in
relation to thermoregulation in endotherms. J Comp Physiol B.
155:711–715. 1985. View Article : Google Scholar : PubMed/NCBI
|
|
58
|
Geiser F and McMurchie EJ: Differences in
the thermotropic behavior of mitochondrial membrane respiratory
enzymes from homeothermic and heterothermic endotherms. J Comp
Physiol B. 155:125–133. 1984. View Article : Google Scholar
|
|
59
|
Oleson JR, Calderwood SK, Coughlin CT,
Dewhirst MW, Gerweck LE, Gibbs FA Jr and Kapp DS: Biological and
clinical aspects of hyperthermia in cancer therapy. Am J Clin
Oncol. 11:368–380. 1988. View Article : Google Scholar : PubMed/NCBI
|
|
60
|
Laider KJ: The development of the
Arrhenius equation. J Chem Educ. 61:494–498. 1984. View Article : Google Scholar
|
|
61
|
Gardiner WC Jr: Temperature dependence of
bimolecular gas reaction rates. Acc Chem Res. 10:326–331. 1977.
View Article : Google Scholar
|
|
62
|
Petrou AL, Roulia M and Tampouris K: The
use of the Arrhenius equation in the study of deterioration and of
cooking of foods - some scientific and pedagogic aspects. Chem Educ
Res And Pract In Eur. 3:87–97. 2002. View Article : Google Scholar
|
|
63
|
Qin Z, Balasubramanian SK, Wolkers WF,
Pearce JA and Bischof JC: Correlated parameter fit of arrhenius
model for thermal denaturation of proteins and cells. Ann Biomed
Eng. 42:2392–2404. 2014. View Article : Google Scholar : PubMed/NCBI
|
|
64
|
Whitney J, Carswell W and Rylander N:
Arrhenius parameter determination as a function of heating method
and cellular microenvironment based on spatial cell viability
analysis. Int J Hyperthermia. 29:281–295. 2013. View Article : Google Scholar : PubMed/NCBI
|
|
65
|
Scalley ML and Baker D: Protein folding
kinetics exhibit an Arrhenius temperature dependence when corrected
for the temperature dependence of protein stability. Proc Natl Acad
Sci USA. 94:10636–10640. 1997. View Article : Google Scholar : PubMed/NCBI
|
|
66
|
Abney JR and Owicki JC: Theories of
protein-lipid and protein-protein interactions in membranes.
Progress in Protein-Lipid Interactions. Watts A and de Pont JJ: 1.
Elsevier Biomedical Press; Amsterdam: pp. 1–60. 1985
|
|
67
|
Evans MG and Polanyi M: Some applications
of the transition state method to the calculation of reaction
velocities, especially in solution. Trans Faraday Soc. 31:875–894.
1935. View Article : Google Scholar
|
|
68
|
Eyring H: The activated complex in
chemical reactions. J Chem Phys. 3:107–115. 1935. View Article : Google Scholar
|
|
69
|
Laidler KJ and King MC: The development of
transition-state theory. J Phys Chem. 87:2657–2664. 1983.
View Article : Google Scholar
|
|
70
|
McRae DA and Esrick MA: Changes in
electrical impedance of skeletal muscle measured during
hyperthermia. Int J Hyperthermia. 9:247–261. 1993. View Article : Google Scholar : PubMed/NCBI
|
|
71
|
Pearce JA: Improving accuracy in arrhenius
models of cell death: Adding a temperature-dependent time delay.
Transactions of the ASME. J Biomech Eng. 137:1210062015. View Article : Google Scholar
|
|
72
|
Eyring H, Gershinowitz H and Sun CE: The
absolute rate of homogeneous atomic reactions. J Chem Phys.
3:786–796. 1935. View Article : Google Scholar
|
|
73
|
Wynne-Jones WF and Eyring H: The absolute
rate of reactions in condensed phases. J Chem Phys. 3:492–502.
1935. View Article : Google Scholar
|
|
74
|
Eyring H and Polanyi M: Über Einfache
Gasreaktionen. Z Phys Chem B. 12:279–311. 1931.In German.
|
|
75
|
Eyring H and Stearn AE: The application of
the theory of absolute reaction rates to proteins. Chem Rev.
24:253–270. 1939. View Article : Google Scholar
|
|
76
|
Crawford BL Jr: Quantum Chemistry. Eyring
Henry, Walter John and Kimball George E.: J Phys Chem. 49:168.
1945. View Article : Google Scholar
|
|
77
|
Szasz A, Szasz N and Szasz O: Oncothermia
- Principles principles and practices. Springer; Science,
Heidelberg: 2010
|
|
78
|
Wright NT: On a relationship between the
Arrhenius parameters from thermal damage studies. J Biomech Eng.
125:300–304. 2003. View Article : Google Scholar : PubMed/NCBI
|
|
79
|
He X: Thermostability of biological
systems: Fundamentals, challenges, and quantification. Open Biomed
Eng J. 5:47–73. 2011. View Article : Google Scholar : PubMed/NCBI
|
|
80
|
He X and Bischof JC: Quantification of
temperature and injury response in thermal therapy and cryosurgery.
Crit Rev Biomed Eng. 31:355–422. 2003. View Article : Google Scholar
|
|
81
|
Jacques SL: Ratio of entropy to enthalpy
in thermal transitions in biological tissues. J Biomed Opt.
11:0411082006. View Article : Google Scholar : PubMed/NCBI
|
|
82
|
Rosenberg B, Kemeny G, Switzer RC and
Hamilton TC: Quantitative evidence for protein denaturation as the
cause of thermal death. Nature. 232:471–473. 1971. View Article : Google Scholar : PubMed/NCBI
|
|
83
|
Low PS, Bada JL and Somero GN: Temperature
adaptation of enzymes: Roles of the free energy, the enthalpy, and
the entropy of activation. Proc Natl Acad Sci USA. 70:430–432.
1973. View Article : Google Scholar : PubMed/NCBI
|
|
84
|
Pearce JA: Thermal dose models:
Irreversible alterations in tissues. Physics of Thermal Therapy,
Fundamentals and Clinical Applications. Moros EG: CRC Press Taylor
and Francis Group; Boca Raton, FL: 2013
|
|
85
|
Lee SY, Kim JH, Han YH and Cho DH: The
effect of modulated electro-hyperthermia on temperature and blood
flow in human cervical carcinoma. Int J Hyperthermia. 34:953–960.
2018. View Article : Google Scholar : PubMed/NCBI
|
|
86
|
Lee SY, Lee NR, Cho DH and Kim JS:
Treatment outcome analysis of chemotherapy combined with modulated
electro- hyperthermia compared with chemotherapy alone for
recurrent cervical cancer, following irradiation. Oncol Lett.
14:73–78. 2017. View Article : Google Scholar : PubMed/NCBI
|
|
87
|
Szasz O, Szasz MA, Minnaar C and Szasz A:
Heating preciosity: Trends in modern oncological hyperthermia. Open
J Biophys. 7:116–144. 2017. View Article : Google Scholar
|
|
88
|
Szent-Gyoergyi A: Cell division and
cancer. Science. 149:34–37. 1965. View Article : Google Scholar : PubMed/NCBI
|
|
89
|
Davies PC, Demetrius L and Tuszynski JA:
Cancer as a dynamical phase transition. Theor Biol Med Model.
8:302011. View Article : Google Scholar : PubMed/NCBI
|
|
90
|
Alfarouk KO, Shayoub ME, Muddathir AK,
Elhassan GO and Bashir AH: Evolution of tumor metabolism might
reflect carcinogenesis as a reverse evolution process (dismantling
of multi-cellularity). Cancers (Basel). 3:3002–3017. 2011.
View Article : Google Scholar
|
|
91
|
Greaves M: Evolutionary determinants of
cancer. Cancer Discov. 5:806–820. 2015. View Article : Google Scholar : PubMed/NCBI
|
|
92
|
Bussey KJ, Cisneros LH, Lineweaver CH and
Davies PC: Ancestral gene regulatory networks drive cancer. Proc
Natl Acad Sci USA. 114:6160–6162. 2015. View Article : Google Scholar
|
|
93
|
Davies PC and Lineweaver CH: Cancer tumors
as Metazoa 1.0: Tapping genes of ancient ancestors. Phys Biol.
8:0150012011. View Article : Google Scholar : PubMed/NCBI
|
|
94
|
Warburg O: Oxygen, the Creator of
Differentiation, Biochemical Energetics. Academic Press; New York
NY: 1966, Warburg O: The Prime Cause and Prevention of Cancer,
Revised lecture at the meeting of the Nobel-Laureates on June 30,
1966 at Lindau, Lake Constance, Germany, 1966.
|
|
95
|
Oehr P, Biersack HJ and Coleman RE: PET
and PET-CT in Oncology. Springer Verlag; Berlin, Heidelberg: 2004,
View Article : Google Scholar
|
|
96
|
Mikac U, Demsar F, Beravs K and Sersa I:
Magnetic resonance imaging of alternating electric currents. Magn
Reson Imaging. 19:845–856. 2001. View Article : Google Scholar : PubMed/NCBI
|
|
97
|
Szasz A, Vincze Gy, Szasz O and Szasz N:
An energy analysis of extracellular hyperthermia. Electromagn Biol
Med. 22:103–115. 2003. View Article : Google Scholar
|
|
98
|
Szentgyorgyi A: Bioelectronics: A Study on
Cellular Regulations, Defense and Cancer. Academic Press; London:
pp. 1968
|
|
99
|
Foster KR and Schepps JL: Dielectric
properties of tumor and normal tissues at radio through microwave
frequencies. J Microw Power. 16:107–119. 1981. View Article : Google Scholar : PubMed/NCBI
|
|
100
|
Blad B and Baldetorp B: Impedance spectra
of tumour tissue in comparison with normal tissue; a possible
clinical application for electric impedance tomography. Physiol
Meas. 17(Suppl 4A): A105–A115. 1996. View Article : Google Scholar
|
|
101
|
Babaeizadeh S, Brooks DH and Isaacson D:
3-D electrical impedance tomography for piecewise constant domains
with known internal boundaries. IEEE Trans Biomed Eng. 54:2–10.
2007. View Article : Google Scholar : PubMed/NCBI
|
|
102
|
Scholz B and Anderson R: On electrical
impedance scanning - Principles and simulations. Electromedica.
68:35–44. 2000.
|
|
103
|
Musha T and Sawada Y: Physics of the
Living Atate. IOS Press; Amsterdam: 1994
|
|
104
|
West BJ: Fractal Physiology and Chaos in
Medicine. World Scientific; London: 1990, View Article : Google Scholar
|
|
105
|
Lovelady DC, Richmond TC, Maggi AN, Lo CM
and Rabson DA: Distinguishing cancerous from noncancerous cells
through analysis of electrical noise. Phys Rev E Stat Nonlin Soft
Matter Phys. 76:0419082007. View Article : Google Scholar : PubMed/NCBI
|
|
106
|
Szasz O, Andocs G and Meggyeshazi N:
Modulation effect in oncothermia. Hindawi Publishing Corporation
Conference Papers in Medicine. 2013.e3956782013.
|
|
107
|
Szasz A, Szasz N and Szasz O: Oncothermia
- Principles and practices. Springer Science; Heidelberg: pp.
2202010
|
|
108
|
Yang KL, Huang CC, Chi MS, Chiang HC, Wang
YS, Andocs G, et al: In vitro comparison of conventional
hyper-thermia and modulated electro-hyperthermia. Oncotarget.
7:84082–84092. 2016.PubMed/NCBI
|
|
109
|
Pethig R: Dielectric properties of
biological materials: Biophysical and medical applications. IEEE
Transactions on Electrical Insulation. E1–19. 453–474. 1984.
|
|
110
|
Schwan HP: Determination of biological
impedances. Physical Techniques in Biological Research. 6. Academic
Press; New York NY: pp. 323–406. 1963
|
|
111
|
Pennock BE and Schwan HP: Further
observations on the electrical properties of hemoglobin-bound
water. J Phys Chem. 73:2600–2610. 1969. View Article : Google Scholar : PubMed/NCBI
|
|
112
|
Szasz O and Szasz A: Oncothermia -
nano-heating paradigm. J Cancer Sci Ther. 6:42014. View Article : Google Scholar
|
|
113
|
Vincze Gy, Szigeti Gy, Andocs G and Szasz
A: Nanoheating without artificial nanoparticles. Biol Med
(Aligarh). 7:2492015.
|
|
114
|
Szasz A: Electromagnetic effects in
nanoscale range. Cellular Response to Physical Stress and
Therapeutic Applications. Shimizu T and Kondo T: Nova Science
Publishers Inc.; Hauppauge, NY: 2013
|
|
115
|
Andocs G, Rehman MU, Zhao QL, Papp E,
Kondo T and Szasz A: Nanoheating without artificial nanoparticles
Part II. Experimental support of the nanoheating concept of the
modulated electro- hyperthermia method, using U937 cell suspension
model. Biol Med (Aligarh). 7:1–9. 2015. View Article : Google Scholar
|
|
116
|
Andocs G, Rehman MU, Zhao QL, Tabuchi Y,
Kanamori M and Kondo T: Comparison of biological effects of
modulated electro-hyperthermia and conventional heat treatment in
human lymphoma U937 cells. Cell Death Discov. 2:160392016.
View Article : Google Scholar : PubMed/NCBI
|
|
117
|
Andocs G, Renner H, Balogh L, Fonyad L,
Jakab C and Szasz A: Strong synergy of heat and modulated
electro-magnetic field in tumor cell killing, Study of HT29
xenograft tumors in a nude mice model. Strahlenther Onkol.
185:120–126. 2009. View Article : Google Scholar : PubMed/NCBI
|
|
118
|
Andocs G, Okamoto Y, Osaki T, Tsuka T,
Imagawa T, Minami S, Balogh L, Meggyeshazi N and Szasz O:
Oncothermia research at preclinical level. Hindawi Publishing
Corporation Conference Papers in Medicine; 2013, pp.
e2724672013
|
|
119
|
Szasz A: Current status of oncothermia
therapy for lung cancer. Korean J Thorac Cardiovasc Surg. 47:77–93.
2014. View Article : Google Scholar : PubMed/NCBI
|
|
120
|
Meggyeshazi N: Studies on modulated
electrohyperthermia induced tumor cell death in a colorectal
carcinoma model. PhD Theses. Pathological Sciences Doctoral School,
Semmelweis University; Budapest: 2015
|
|
121
|
Meggyeshazi N, Andocs G, Balogh L, Balla
P, Kiszner G, Teleki I, Jeney A and Krenacs T: DNA fragmentation
and caspase-independent programmed cell death by modulated
electrohyperthermia. Strahlenther Onkol. 190:815–822. 2014.
View Article : Google Scholar : PubMed/NCBI
|
|
122
|
Andocs G, Meggyeshazi N, Balogh L, Spisak
S, Maros ME, Balla P, Kiszner G, Teleki I, Kovago C and Krenacs T:
Upregulation of heat shock proteins and the promotion of damage-
associated molecular pattern signals in a colorectal cancer model
by modulated electrohyperthermia. Cell Stress Chaperones. 20:37–46.
2015. View Article : Google Scholar
|
|
123
|
Qin W, Akutsu Y, Andocs G, Suganami A, Hu
X, Yusup G, Komatsu-Akimoto A, Hoshino I, Hanari N, Mori M, et al:
Modulated electro-hyperthermia enhances dendritic cell therapy
through an abscopal effect in mice. Oncol Rep. 32:2373–2379. 2014.
View Article : Google Scholar : PubMed/NCBI
|
|
124
|
Tsang YW, Huang CC, Yang KL, Chi MS,
Chiang HC, Wang YS, Andocs G, Szasz A, Li WT and Chi KH: Improving
immunological tumor microenvironment using electro-hyperthermia
followed by dendritic cell immunotherapy. BMC Cancer. 15:7082015.
View Article : Google Scholar : PubMed/NCBI
|
|
125
|
Szasz O and Szasz A: Heating, efficacy and
dose of local hyperthermia. Open J Biophys. 6:10–18. 2016.
View Article : Google Scholar
|
|
126
|
Elmore S: Apoptosis: A review of
programmed cell death. Toxicol Pathol. 35:495–516. 2007. View Article : Google Scholar : PubMed/NCBI
|
|
127
|
Chang LK, Putcha GV, Deshmukh M and
Johnson EM Jr: Mitochondrial involvement in the point of no return
in neuronal apoptosis. Biochimie. 84:223–231. 2002. View Article : Google Scholar : PubMed/NCBI
|
|
128
|
Langdon BB, Kastantin M and Schwartz DK:
Apparent activation energies associated with protein dynamics on
hydrophobic and hydrophilic surfaces. Biophys J. 102:2625–2633.
2012. View Article : Google Scholar : PubMed/NCBI
|
|
129
|
Melnick RL, Hanson RM and Morris HP:
Membranous effects on adenosine triphosphatase activities of
mitochondria from rat liver and Morris hepatoma 3924A. Cancer Res.
37:4395–4399. 1977.PubMed/NCBI
|
|
130
|
Kushnareva Y, Andreyev AY, Kuwana T and
Newmeyer DD: Bax activation initiates the assembly of a multimeric
catalyst that facilitates Bax pore formation in mitochondrial outer
membranes. PLoS Biol. 10:e10013942012. View Article : Google Scholar : PubMed/NCBI
|
|
131
|
Pouliquen D, Bellot G, Guihard G, Fichet
P, Meflah K and Vallette FM: Mitochondrial membrane
permeabilization produced by PTP, Bax and apoptosis: A 1H-NMR
relaxation study. Cell Death Differ. 13:301–310. 2006. View Article : Google Scholar
|
|
132
|
De Virville JD, Cantrel C, Bousquet AL,
Hoffelt M, Tenreiro AM, Vaz Pinto V, Arrabaca JD, Caiveau O, Moreau
F and Zachowski A: Homeoviscous and functional adaptations of
mitochondrial membranes to growth temperature in soybean seedlings.
Plant Cell Environ. 25:1289–1297. 2002. View Article : Google Scholar
|
|
133
|
Lenaz G, Sechi AM, Parenti-Castelli G,
Landi L and Bertoli E: Activation energies of different
mitochondrial enzymes: Breaks in Arrhenius plots of membrane-bound
enzymes occur at different temperatures. Biochem Biophys Res
Commun. 49:536–542. 1972. View Article : Google Scholar : PubMed/NCBI
|
|
134
|
Lee M and Vasioukhin V: Cell polarity and
cancer - cell and tissue polarity as a non-canonical tumor
suppressor. J Cell Sci. 121:1141–1150. 2008. View Article : Google Scholar : PubMed/NCBI
|
|
135
|
Litovitz TA, Krause D, Penafiel M, Elson
EC and Mullins JM: The role of coherence time in the effect of
microwaves on ornithine decarboxylase activity.
Bioelectromagnetics. 14:395–403. 1993. View Article : Google Scholar : PubMed/NCBI
|
|
136
|
Kim EK and Choi EJ: Pathological roles of
MAPK signaling pathways in human diseases. Biochim Biophys Acta.
1802.396–405. 2010.
|
|
137
|
Leszczynski D, Joenväärä S, Reivinen J and
Kuokka R: Non-thermal activation of the hsp27/p38MAPK stress
pathway by mobile phone radiation in human endothelial cells:
Molecular mechanism for cancer- and blood-brain barrier-related
effects. Differentiation. 70:120–129. 2002. View Article : Google Scholar : PubMed/NCBI
|
|
138
|
Cuesta-López S, Errami J, Falo F and
Peyrard M: Can we model DNA at the mesoscale. J Biol Phys.
31:273–301. 2005. View Article : Google Scholar
|
|
139
|
Takahashi A, Matsumoto H, Nagayama K,
Kitano M, Hirose S, Tanaka H, Mori E, Yamakawa N, Yasumoto J, Yuki
K, et al: Evidence for the involvement of double-strand breaks in
heat- induced cell killing. Cancer Res. 64:8839–8845. 2004.
View Article : Google Scholar : PubMed/NCBI
|
|
140
|
Kim JK, Prasad B and Kim S: Temperature
mapping and thermal dose calculation in combined radiation therapy
and 1356 MHz radiofrequency hyperthermia for tumor treatment Proc
SPIE 10047. Opt Methods Tumor Treat Detect Mech Tech Photodynamic
Ther. 26:10047182017.
|
|
141
|
Szasz O, Andocs G and Meggyeshazi N:
Oncothermia as Personalized Treatment Option. Hindawi Publishing
Corporation Conference Papers in Medicine 2013. e29413642013.
|
|
142
|
Fowler JF: The first James Kirk memorial
lecture. What next in fractionated radiotherapy. Br J Cancer.
6:285–300. 1984.
|
|
143
|
Wang JZ, Li XA, D'Souza WD and Stewart RD:
Impact of prolonged fraction delivery times on tumor control: A
note of caution for intensity-modulated radiation therapy (IMRT).
Int J Radiat Oncol Biol Phys. 57:543–552. 2003. View Article : Google Scholar : PubMed/NCBI
|
|
144
|
Angus SD and Piotrowska MJ: A matter of
timing: identifying significant multi-dose radiotherapy
improvements by numerical simulation and genetic algorithm search.
PLoS One. 9:e1140982014. View Article : Google Scholar : PubMed/NCBI
|
|
145
|
Andocs G, Okamoto Y, Kawamoto K, Osaki T,
Tsuka T, Imagawa T, Miniami S, Balogh L, Meggysházi N and Szasz O:
Oncothermia basic research at in vivo level The first results in
Japan. Hindawi Publishing Corporation Conference Papers in Medicine
2013. e1973282013.
|
|
146
|
Kim W, Kim MS, Kim HJ, Lee E, Jeong JH,
Park I, Jeong YK and Jang WI: Role of HIF-1α in response of tumors
to a combination of hyperthermia and radiation in vivo. Int J
Hyperthermia. 28:1–8. 2017.
|
|
147
|
Lee SY and Kim MG: The effect of modulated
electro-hyperthermia on the pharmacokinetic properties of nefopam
in healthy volunteers: A randomised, single-dose, crossover
open-label study. Int J Hyperthermia. 31:869–874. 2015. View Article : Google Scholar : PubMed/NCBI
|
|
148
|
Meggyeshazi N, Andocs G and Krenacs T:
Programmed cell death induced by modulated electro-hyperthermia.
Hindawi Publishing Corporation Conference Papers in Medicine 2013.
e187835.2013.
|